Μέχρι στιγμής έχουμε δει ουσιαστικά δύο κατηγορίες γλωσσών: τις κανονικές (regular) γλώσσες και τις context free γλώσσες. Η πρώτη κατηγορία περιέχεται στη δεύτερη. Από τη μέχρι στιγμής παρουσίαση πρέπει να έχει φανεί καθαρά ότι για κάθε μια από τις δύο κατηγορίες υπάρχει και ένα αντίστοιχο υπολογιστικό μοντέλο: τα πεπερασμένα αυτόματα (ντετερμινιστικά ή μη) για τις κανονικές γλώσσες και τα αυτόματα με στοίβα (push-down automata) για τις context free γλωσσες. Η αντιστοιχία στην οποία αναφερθήκαμε είναι ότι μια γλώσσα είναι στην κατηγορία που εξετάζουμε (κανονική ή context-free) αν και μόνο αν υπάρχει μια μηχανή του αντίστοιχου τύπου (πεπερασμένο αυτόματο ή αυτόματο με στοίβα) που αναγνωρίζει τη γλώσσα αυτή.
Είδαμε ότι το να υπάρχει ένα DFA για μια γλώσσα ![]() είναι ισοδύναμο με το
μπορεί κανείς να γράψει ένα πρόγραμμα σε μια γλώσσα προγραμματισμού (ας πούμε σε C)
που να αναγνωρίζει τις λέξεις της
είναι ισοδύναμο με το
μπορεί κανείς να γράψει ένα πρόγραμμα σε μια γλώσσα προγραμματισμού (ας πούμε σε C)
που να αναγνωρίζει τις λέξεις της ![]() (να επιστρέφει δηλ. το πρόγραμμα αυτό 1 αν η λέξη
που του δώσαμε ανήκει στην
(να επιστρέφει δηλ. το πρόγραμμα αυτό 1 αν η λέξη
που του δώσαμε ανήκει στην ![]() και 0 αλλιώς), το οποίο δε χρησιμοποιεί απεριόριστη μνήμη αλλά
μνήμη μεγέθους σταθερού και προκαθορισμένου, το ίδιο για όλες τις λέξεις της
και 0 αλλιώς), το οποίο δε χρησιμοποιεί απεριόριστη μνήμη αλλά
μνήμη μεγέθους σταθερού και προκαθορισμένου, το ίδιο για όλες τις λέξεις της ![]() .
Ισοδύναμα, μιλάμε για ένα πρόγραμμα σε C που χρησιμοποιεί ένα στεθερό αριθμό μεταβλητών
(όχι πίνακες) η καθεμία από τις οποίες χρησιμοποιεί προκαθορισμένη μνήμη (π.χ. ακέραιοι
των 32 bits - δυαδικών ψηφίων).
.
Ισοδύναμα, μιλάμε για ένα πρόγραμμα σε C που χρησιμοποιεί ένα στεθερό αριθμό μεταβλητών
(όχι πίνακες) η καθεμία από τις οποίες χρησιμοποιεί προκαθορισμένη μνήμη (π.χ. ακέραιοι
των 32 bits - δυαδικών ψηφίων).
Αντίστοιχα, ένα ντετερμινιστικό αυτόματο με στοίβα είναι ακριβώς ένα πρόγραμμα σε C που χρησιμοποιεί μεν πεπερασμένη μνήμη μόνο, αλλά έχει και πρόσβαση σε μια άπειρη στοίβα με ένα περιορισμένο όμως τρόπο, που του επιτρέπει να διαβάζει και να τροποποιεί πάντα μόνο την κορυφή της στοίβας. Τα ντετερμινιστικά αυτόματα με στοίβα δεν αρκούν για να αναγνωρίσουν όλες τις context free γλώσσες όμως, αλλά μπορεί κανείς με λίγη προσοχή να δείξει ότι και τα μη ντετερμιστικά αυτόματα με στοίβα έχουν ισοδύναμα C προγράμματα.
Είναι πλέον φυσιολογικός ο ακόλουθος ορισμός.
Ας παρατηρήσουμε εδώ ότι δεν υπάρχει κάτι μαγικό που να μας επιβάλλει το ![]() σα πεδίο ορισμού και πεδίο τιμών στον παραπάνω ορισμό. Στη θέση του θα μπορούσε
να είναι οποιοδήποτε σύνολο που τα στοιχεία του να μπορούν να παρασταθούν, με κάποιο
τρόπο, στον υπολογιστή (ένα τέτοιο σύνολο δεν είναι το σύνολο
σα πεδίο ορισμού και πεδίο τιμών στον παραπάνω ορισμό. Στη θέση του θα μπορούσε
να είναι οποιοδήποτε σύνολο που τα στοιχεία του να μπορούν να παρασταθούν, με κάποιο
τρόπο, στον υπολογιστή (ένα τέτοιο σύνολο δεν είναι το σύνολο
![]() των πραγματικών αριθμών).
Αυτό όμως σημαίνει ουσιαστικά ότι μπορούμε να γράψουμε κάτω μια λέξη
από 0 ή 1 που να αντστοιχεί μοναδικά σε ένα στοιχείο του συνόλου αυτού.
Πολλές φορές βλέπει κανείς τον ορισμό της υπολογίσιμης συνάρτησης να δίνεται π.χ. για
συναρτήσεις από τους φυσικούς αριθμούς στους φυσικούς.
Εμείς με τον όρο υπολογίσιμη συνάρτηση θα καταλαβαίνουμε οποιαδήποτε απεικόνιση
την οποία μπορούμε να υπολογίζουμε χρησιμοποιώντας ένα πρόγραμμα.
των πραγματικών αριθμών).
Αυτό όμως σημαίνει ουσιαστικά ότι μπορούμε να γράψουμε κάτω μια λέξη
από 0 ή 1 που να αντστοιχεί μοναδικά σε ένα στοιχείο του συνόλου αυτού.
Πολλές φορές βλέπει κανείς τον ορισμό της υπολογίσιμης συνάρτησης να δίνεται π.χ. για
συναρτήσεις από τους φυσικούς αριθμούς στους φυσικούς.
Εμείς με τον όρο υπολογίσιμη συνάρτηση θα καταλαβαίνουμε οποιαδήποτε απεικόνιση
την οποία μπορούμε να υπολογίζουμε χρησιμοποιώντας ένα πρόγραμμα.
Για παράδειγμα οι παρακάτω συναρτήσεις είναι υπολογίσιμες αφού εύκολα βλέπει
κανείς ότι υπάρχουν προγράμματα που τις υπολογίζουν.
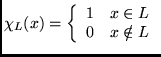
Είναι τώρα φανερό ότι οι κανονικές και οι context free γλώσσες είναι αναδρομικά σύνολα, αφού υπάρχουν προγράμματα που τις ``αποφασίζουν''. Η ιεραρχία των γλωσσών που έχουμε μέχρι τώρα δεί λοιπόν είναι η
(κανονικές γλώσσες)Και οι δύο παραπάνω εγκλεισμοί είναι γνήσιοι, υπάρχει δηλ. context free γλώσσα που δεν είναι κανονική (π.χ. η γλώσσα των παλίνδρομων λέξεων(context free γλώσσες)
(αναδρομικές γλώσσες).
Είναι σημαντικό να τονίσουμε εδώ ότι η μεταβλητή του C προγράμματος όπου
κρατιέται, π.χ., το πλήθος των ![]() , είναι μια μεταβλητή για την οποία χρειαζόμαστε
απεριόριστη μνήμη. Δεν είναι δηλ. δυνατόν να προκαθορίσουμε ένα άνω όριο για
το πλήθος αυτό. Και επειδή ο φυσικός αριθμός
, είναι μια μεταβλητή για την οποία χρειαζόμαστε
απεριόριστη μνήμη. Δεν είναι δηλ. δυνατόν να προκαθορίσουμε ένα άνω όριο για
το πλήθος αυτό. Και επειδή ο φυσικός αριθμός ![]() χρειάζεται περίπου
χρειάζεται περίπου
![]() δυαδικά ψηφία για να παρασταθεί στον υπολογιστή, κι επειδή η συνάρτηση
δυαδικά ψηφία για να παρασταθεί στον υπολογιστή, κι επειδή η συνάρτηση
![]() αυξάνει (αν και αργά) χωρίς όριο όταν
αυξάνει (αν και αργά) χωρίς όριο όταν
![]() ,
αυτό το C πρόγραμμα δεν χρησιμοποιεί σταθερή μνήμη (αν αυτό συνέβαινε τότε
η γλώσσα αυτή θα ήταν κανονική, ενώ δεν είναι καν context free).
,
αυτό το C πρόγραμμα δεν χρησιμοποιεί σταθερή μνήμη (αν αυτό συνέβαινε τότε
η γλώσσα αυτή θα ήταν κανονική, ενώ δεν είναι καν context free).
Είναι πολύ φυσιολογικό το ερώτημα αν υπάρχουν συναρτήσεις που
να μην είναι υπολογίσιμες. Για να συγκεκριμενοποιήσουμε τα πράγματα,
ένα φυσιολογικό ερώτημα είναι αν υπάρχει συνάρτηση
![]() για
την οποία να μη μπορούμε να γράψουμε ένα πρόγραμμα που να την υπολογίζει.
για
την οποία να μη μπορούμε να γράψουμε ένα πρόγραμμα που να την υπολογίζει.
Γιατί είναι τώρα το σύνολο όλων των προγραμμάτων αριθμήσιμο;
Απλούστατα, κάθε πρόγραμμα δεν είναι παρά μια, συνήθως μεγάλη, λέξη
πάνω από ένα συγκεκριμένο αλφάβητο ![]() . Για παράδειγμα, όλα τα προγράμματα
σε C γράφονται στο αλφάβητο που χρησιμοποιούν οι σύγχρονοι
υπολογιστές και που περιλαμβάνει όλα τα λατινικά γράμματα,
μικρά και κεφαλαία, δίαφορα σημεία στίξης, αριθμητικούς και άλλους τελεστές,
ψηφία, κλπ. Απαριθμούμε πρώτα λοιπόν όλες τις λέξεις μήκους 1, μετά όλες τις λέξεις
μήκους 2, όλες τις λέξεις μήκους 3, κ.ο.κ., και για κάθε λέξη που
παράγουμε την αναφέρουμε στη λίστα των προγραμμάτων, αν αυτή είναι πρόγραμμα
(πληροί δηλ. τους συντακτικούς κανόνες της γλώσσας προγραμματισμού που
χρησιμοποιούμε). Μπορούμε να το κάνουμε αυτό ακριβώς επειδή όλες οι λέξεις
πάνω από το
. Για παράδειγμα, όλα τα προγράμματα
σε C γράφονται στο αλφάβητο που χρησιμοποιούν οι σύγχρονοι
υπολογιστές και που περιλαμβάνει όλα τα λατινικά γράμματα,
μικρά και κεφαλαία, δίαφορα σημεία στίξης, αριθμητικούς και άλλους τελεστές,
ψηφία, κλπ. Απαριθμούμε πρώτα λοιπόν όλες τις λέξεις μήκους 1, μετά όλες τις λέξεις
μήκους 2, όλες τις λέξεις μήκους 3, κ.ο.κ., και για κάθε λέξη που
παράγουμε την αναφέρουμε στη λίστα των προγραμμάτων, αν αυτή είναι πρόγραμμα
(πληροί δηλ. τους συντακτικούς κανόνες της γλώσσας προγραμματισμού που
χρησιμοποιούμε). Μπορούμε να το κάνουμε αυτό ακριβώς επειδή όλες οι λέξεις
πάνω από το ![]() μήκους
μήκους ![]() είναι φυσικά πεπερασμένες το πλήθος, και άρα κάποια
στιγμή τελειώνουμε την απαρίθμηση των λέξεων μήκους
είναι φυσικά πεπερασμένες το πλήθος, και άρα κάποια
στιγμή τελειώνουμε την απαρίθμηση των λέξεων μήκους ![]() και προχωράμε στην
απαρίθμηση των λέξεων μήκους
και προχωράμε στην
απαρίθμηση των λέξεων μήκους ![]() .
Κάθε πρόγραμμα λοιπόν θα εμφανιστεί στη λίστα μας κάποια στιγμή ανάλογα και
με το ποιο είναι το μήκος του. Έχουμε λοιπόν μέχρι στιγμής δείξει
ότι το πλήθος όλων των υπολογισίμων συναρτήσεων είναι αριθμήσιμο.
.
Κάθε πρόγραμμα λοιπόν θα εμφανιστεί στη λίστα μας κάποια στιγμή ανάλογα και
με το ποιο είναι το μήκος του. Έχουμε λοιπόν μέχρι στιγμής δείξει
ότι το πλήθος όλων των υπολογισίμων συναρτήσεων είναι αριθμήσιμο.
Η απόδειξη του θεωρήματος συμπληρώνεται από το ότι το πλήθος όλων
των συναρτήσεων από το
![]() στο
στο
![]() δεν είναι αριθμήσιμο, δε μπορούμε δηλ. να
διατάξουμε όλες αυτές τις συναρτήσεις σε μια ακολουθία
δεν είναι αριθμήσιμο, δε μπορούμε δηλ. να
διατάξουμε όλες αυτές τις συναρτήσεις σε μια ακολουθία
Στην παραπάνω απόδειξη δείξαμε ότι υπάρχουν μη υπολογίσιμες συναρτήσεις δείχνοντας ότι το σύνολο των υπολογισίμων συναρτήσεων είναι αριθμήσιμο ενώ, αντίθετα, το σύνολο όλων των συναρτήσεων δεν είναι, είναι αυτό που λέμε υπεραριθμήσιμο σύνολο. Άρα, δεν μπορούν τα δύο σύνολα να είναι ίσα.
Αυτός είναι ένας κλασικός τρόπος απόδειξης στα μαθηματικά, η ``υπαρξιακή απόδειξη'', που αν και είναι αρκετά εύκολος και αποδεικνύει αυτό που θέλουμε, δεν είναι τόσο ικανοποιητικός επειδή αποδεικνύεται η ύπαρξη ενός αντικειμένου με ορισμένες ιδιότητες, αλλά, συνήθως, δεν προσδιορίζεται με κάποιο τρόπο κάποιο τέτοιο αντικείμενο. Στην προκειμένη περίπτωση γνωρίζουμε πλέον, μετά την απόδειξη του Θεωρήματος 12, ότι υπάρχουν συναρτήσεις από τους φυσικούς στους φυσικούς που δεν είναι υπολογίσιμες, αλλά δε γνωρίζουμε καμία συγκεκριμένη τέτοια συνάρτηση. Θα δούμε αργότερα συγκεκριμένα παραδείγματα που για το καθένα θα έχουμε και ιδιαίτερο τρόπο απόδειξης του ότι δεν είναι υπολογίσιμα.
Τα προγράμματα ως αριθμοί, και το αντίστροφο Για τη συζήτηση από δω και πέρα θα χρειαστούμε να βλέπουμε το τυχόν C πρόγραμμα ως ένα φυσικό αριθμό, και τον τυχόντα φυσικό αριθμό ως ένα C πρόγραμμα. Πώς γίνεται αυτό;Πολύ απλά, ένα C πρόγραμμα δεν είναι παρά ένα κομμάτι κειμένου, μια λέξη δηλ. πάνω από ένα συγκεκριμένο αλφάβητο. Το αλφάβητο που χρησιμοποιείται στους υπολογιστές σήμερα είναι το
Η απεικόνιση
![]() είναι εύκολο να δεί κανείς ότι
είναι ένα προς ένα (αλλά όχι επί), και ότι η απεικόνιση
είναι εύκολο να δεί κανείς ότι
είναι ένα προς ένα (αλλά όχι επί), και ότι η απεικόνιση
![]() δεν είναι ένα προς ένα.
Είναι επίσης σημαντικό το ότι και οι δύο απεικονίσεις είναι υπολογίσιμες.
Το ότι η
δεν είναι ένα προς ένα.
Είναι επίσης σημαντικό το ότι και οι δύο απεικονίσεις είναι υπολογίσιμες.
Το ότι η ![]() είναι υπολογίσιμη είναι φανερό, ενώ το μόνο λεπτό
σημείο όσον αφορά την υπολογισιμότητα της
είναι υπολογίσιμη είναι φανερό, ενώ το μόνο λεπτό
σημείο όσον αφορά την υπολογισιμότητα της ![]() είναι στο κομμάτι όπου
πρέπει να ελέγξουμε αν η λέξη του
είναι στο κομμάτι όπου
πρέπει να ελέγξουμε αν η λέξη του ![]() που προκύπτει είναι συντακτικά
σωστό C πρόγραμμα ή όχι. Το να αποδείξουμε ότι κάτι τέτοιο είναι
υπολογστικά εφικτό σημαίνει ουσιαστικά να γράψουμε ένα πρόγραμμα που
να αναγνωρίζει αν ένα κομμάτι κειμένου (μια λέξη του
που προκύπτει είναι συντακτικά
σωστό C πρόγραμμα ή όχι. Το να αποδείξουμε ότι κάτι τέτοιο είναι
υπολογστικά εφικτό σημαίνει ουσιαστικά να γράψουμε ένα πρόγραμμα που
να αναγνωρίζει αν ένα κομμάτι κειμένου (μια λέξη του ![]() ) είναι
ένα σωστό συντακτικά C πρόγραμμα ή όχι. Τέτοια προγράμματα όμως υπάρχουν
και χρησιμοποιούνται ευρέως αφού αποτελούν το πρώτο τμήμα των complilers
(μεταφραστών) που παίρνουν ένα πρόγραμμα σε C και παράγουν από αυτό
ένα ισοδύναμο πρόγραμμα σε ``γλώσσα μηχανής''.
) είναι
ένα σωστό συντακτικά C πρόγραμμα ή όχι. Τέτοια προγράμματα όμως υπάρχουν
και χρησιμοποιούνται ευρέως αφού αποτελούν το πρώτο τμήμα των complilers
(μεταφραστών) που παίρνουν ένα πρόγραμμα σε C και παράγουν από αυτό
ένα ισοδύναμο πρόγραμμα σε ``γλώσσα μηχανής''.
Προσομοίωση.
Θα χρειαστούμε επίσης το εξής: Υπάρχει ένα πρόγραμμα ![]() με παραμέτρους
το οποίο (α) βρίσκει το πρόγραμμα
με παραμέτρους
το οποίο (α) βρίσκει το πρόγραμμα
![]() και (β) ``Τρέχει'' το πρόγραμμα
και (β) ``Τρέχει'' το πρόγραμμα
![]() για τόσα βήματα όσα λέει ο αριθμός
για τόσα βήματα όσα λέει ο αριθμός ![]() ή επ άπειρον αν ο αριθμός
ή επ άπειρον αν ο αριθμός ![]() είναι αρνητικός. Αν και όταν το πρόγραμμα
είναι αρνητικός. Αν και όταν το πρόγραμμα ![]() τελειώσει το
τελειώσει το ![]() επιστρέφει
ότι επέστρεψε το
επιστρέφει
ότι επέστρεψε το ![]() .
Δε θα δείξουμε την ύπαρξη αυτού του προγράμματος που προσμομοιώνει άλλα προγράμματα,
μια και τέτοια προγράμματα υπάρχουν και χρησιμοποιούνται ευρέως στον προγραμματισμό
(π.χ. interpreters, debuggers, κλπ).
.
Δε θα δείξουμε την ύπαρξη αυτού του προγράμματος που προσμομοιώνει άλλα προγράμματα,
μια και τέτοια προγράμματα υπάρχουν και χρησιμοποιούνται ευρέως στον προγραμματισμό
(π.χ. interpreters, debuggers, κλπ).
Είμαστε έτοιμοι τώρα να αναφερθούμε στο Halting problem (πρόβλημα τερματισμού). Αυτό ρωτάει απλά αν υπάρχει ένα πρόγραμμα που να μπορεί να αποφασίζει αν ένα τυχόν άλλο πρόγραμμα που εμείς του προσδιορίζουμε θα τερματίσει ή όχι. (Είναι φανερό ότι υπάρχουν προγράμματα που δεν τερματίζουν ποτέ, π.χ. το main() { while(1) 1; }). Ένα τέτοιο πρόγραμμα θα ήταν εξαιρετικά χρήσιμο αν υπήρχε. Φανταστείτε να έχετε ένα C compiler ο οποίος όχι μόνο θα μετάφραζε το πρόγραμμά σας σε γλώσσα μηχανής αλλά θα μπορούσε και να σας πει εκ των προτέρων αν το πρόγραμμά σας θα έπεφτε σε άπειρο βρόγχο (loop) ή όχι. Δυστυχώς όμως τέτοιο πρόγραμμα δεν υπάρχει.
Στο εξής, για τυχόν πρόγραμμα ![]() , θα γράφουμε
, θα γράφουμε
![]() αν το πρόγραμμα
αν το πρόγραμμα
![]() τερματίζει και
τερματίζει και
![]() αν το
αν το ![]() τρέχει επ' άπειρον.
τρέχει επ' άπειρον.
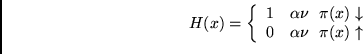
H συνάρτηση ![]() επιστρέφει 1 αν το πρόγραμμα
επιστρέφει 1 αν το πρόγραμμα ![]() τερματίζει και 0 αλλιώς.
τερματίζει και 0 αλλιώς.
Απόδειξη.
Ας υποθέσουμε ότι η συνάρτηση ![]() είναι υπολογίσιμη και ας συμβολίσουμε
με
είναι υπολογίσιμη και ας συμβολίσουμε
με ![]() το πρόγραμμα που την υπολογίζει. Φτιάχνουμε τώρα το πρόγραμμα
το πρόγραμμα που την υπολογίζει. Φτιάχνουμε τώρα το πρόγραμμα ![]() που χρησιμοποιεί το
που χρησιμοποιεί το ![]() ως υποπρόγραμμα:
ως υποπρόγραμμα:
int Q(x)
{
if (P(x
(x))) == 0) return 1;
else {
while(1) 1;
}
}
Το πρόγραμμα ![]() που ορίσαμε έχει την ιδιότητα ότι τερματίζει αν και μόνο αν
το
που ορίσαμε έχει την ιδιότητα ότι τερματίζει αν και μόνο αν
το
![]() δεν τερματίζει. Δηλαδή, δοθέντος του
δεν τερματίζει. Δηλαδή, δοθέντος του
![]() υπολογίζουμε το πρόγραμμα
υπολογίζουμε το πρόγραμμα
![]() που του αντιστοιχεί και του προσδιορίζουμε ως input πάλι τον αριθμό
που του αντιστοιχεί και του προσδιορίζουμε ως input πάλι τον αριθμό ![]() .
Αυτό το νέο πρόγραμμα περνούμε ως παράμετρο στο πρόγραμμα
.
Αυτό το νέο πρόγραμμα περνούμε ως παράμετρο στο πρόγραμμα ![]() .
.
Ποια είναι η συμπεριφορά του προγράμματος
![]() ;
Τερματίζει ή όχι;
Σύμφωνα με τη προηγούμενη παρατήρηση τερματίζει αν και μόνο αν
το πρόγραμμα
;
Τερματίζει ή όχι;
Σύμφωνα με τη προηγούμενη παρατήρηση τερματίζει αν και μόνο αν
το πρόγραμμα
![]() δεν τερματίζει.
Αλλά
δεν τερματίζει.
Αλλά
![]() , οπότε δείξαμε ότι το πρόγραμμα
, οπότε δείξαμε ότι το πρόγραμμα
![]() τερματίζει αν και μόνο αν δεν τερματίζει, πράγμα προφανώς αδύνατο.
Το συμπέρασμα είναι ότι η συνάρτηση
τερματίζει αν και μόνο αν δεν τερματίζει, πράγμα προφανώς αδύνατο.
Το συμπέρασμα είναι ότι η συνάρτηση ![]() δεν είναι υπολογίσιμη.
δεν είναι υπολογίσιμη.
![]()
Έχουμε λοιπόν δείξει ότι η, πολύ φυσιολογική, συνάρτηση ![]() που διακρίνει πότε το πρόγραμμα
που διακρίνει πότε το πρόγραμμα ![]() τερματίζει ή όχι δεν είναι υπολογίσιμη.
Έχουμε λοιπόν τώρα μια απόδειξη του ότι υπάρχουν μη υπολογίσιμες
συναρτήσεις που είναι αρκετά πιο συγκεκριμένη από την προηγούμενη
υπαρξιακή απόδειξη του Θεωρήματος 12.
Μπορεί βέβαια και πάλι να πει κανείς ότι η
τερματίζει ή όχι δεν είναι υπολογίσιμη.
Έχουμε λοιπόν τώρα μια απόδειξη του ότι υπάρχουν μη υπολογίσιμες
συναρτήσεις που είναι αρκετά πιο συγκεκριμένη από την προηγούμενη
υπαρξιακή απόδειξη του Θεωρήματος 12.
Μπορεί βέβαια και πάλι να πει κανείς ότι η ![]() δεν έχει ίσως και τόσο
ενδιαφέρον από μαθηματική άποψη μια και είναι μια συνάρτηση ``κομμένη και ραμμένη''
στα μέτρα της Θεωρίας Υπολογισμών, και άρα όχι, ίσως, τόσο φυσιολογική.
δεν έχει ίσως και τόσο
ενδιαφέρον από μαθηματική άποψη μια και είναι μια συνάρτηση ``κομμένη και ραμμένη''
στα μέτρα της Θεωρίας Υπολογισμών, και άρα όχι, ίσως, τόσο φυσιολογική.
Υπάρχουν όμως πολλά παραδείγματα αρκετά φυσιολογικών μαθηματικών προβλημάτων που δεν επιδέχονται λύση αλγοριθμική, προβλήματα που προϋπήρχαν της Θεωρίας Υπολογισμών.
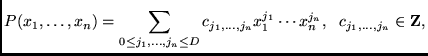
Είναι σχεδόν άμεσο ότι κάθε αναδρομικό σύνολο είναι και α.α.
Πράγματι, αν
![]() είναι αναδρομικό τότε υπάρχει πρόγραμμα
είναι αναδρομικό τότε υπάρχει πρόγραμμα
![]() τέτοιο ώστε
τέτοιο ώστε
![]() .
Τότε το ακόλουθο πρόγραμμα απαριθμεί τα στοιχεία του
.
Τότε το ακόλουθο πρόγραμμα απαριθμεί τα στοιχεία του ![]() (
(![]() είναι, π.χ., το
μικρότερο στοιχείο του
είναι, π.χ., το
μικρότερο στοιχείο του ![]() ):
):
int P(x)
{
if(Q(x)) return x;
else return m;
}
Από την άλλη μεριά είναι εύκολο να κατασκευάσουμε α.α. σύνολα που δεν είναι αναδρομικά. Για παράδειγμα, το σύνολο
Έχουμε λοιπόν δείξει:
(κανονικές γλώσσες)και όλοι οι εγκλεισμοί είναι γνήσιοι.(context free γλώσσες)
(αναδρομικές γλώσσες)
(α.α. γλώσσες)
Η σχέση αναδρομικών και α.α. συνόλων φαίνεται πιο καθαρά στα επόμενα δύο θεωρήματα.
int R(x)
{
int i=1;
label:
if(P(i) == x) return 1;
if(Q(i) == x) return 0;
i = i+1; goto label;
}
Το πρόγραμμα ![]() απλούστατα παράγει όλους τους αριθμούς
απλούστατα παράγει όλους τους αριθμούς
![]() και μόλις εμφανιστεί το
και μόλις εμφανιστεί το ![]() επιστρέφει 0 ή 1 ανάλογα με το αν το
επιστρέφει 0 ή 1 ανάλογα με το αν το ![]() εμφανίστηκε στην έξοδο του
εμφανίστηκε στην έξοδο του
![]() ή του
ή του ![]() .
Είναι σίγουρο ότι το
.
Είναι σίγουρο ότι το ![]() κάποτε θα εμφανιστεί (μια και είτε θα ανήκει στο
κάποτε θα εμφανιστεί (μια και είτε θα ανήκει στο
![]() είτε στο
είτε στο ![]() ) και άρα για κάθε
) και άρα για κάθε ![]() το πρόγραμμα
το πρόγραμμα ![]() τερματίζει.
τερματίζει.
![]()
Απόδειξη:
Έστω ότι το πρόγραμμα ![]() απαριθμεί τα στοιχεία του
απαριθμεί τα στοιχεία του ![]() :
:
int Q(x)
{
int i=1;
label:
if(P(i) == x) return 1;
i = i+1; goto label;
}
Το πρόγραμμα ![]() επιστρέφει 1 αν και μόνο αν το
επιστρέφει 1 αν και μόνο αν το ![]() εμφανιστεί στη λίστα
των τιμών του
εμφανιστεί στη λίστα
των τιμών του ![]() , αλλιώς τρέχει επ' άπειρον.
, αλλιώς τρέχει επ' άπειρον.
![]()