


Next: 5.14 Σεπτέμριος
Up: 5 Ημερολόγιο Μαθήματος (Διδακτικές
Previous: 5.12 Υπολογισιμότητα
Contents
Δείτε εδώ
τους τελικούς βαθμούς του μαθήματος.
Τα θέματα που ρωτήθηκαν ήταν τα παρακάτω 6 προβλήματα (2 ώρες διάρκεια).
- Κατασκευάστε DFA για τις γλώσσες (α) τις λέξεις του
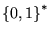 που περιέχουν την υπολέξη 0101
(β)
που περιέχουν την υπολέξη 0101
(β)
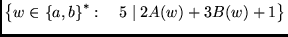 ,
όπου
,
όπου 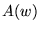 , και
, και 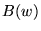 είναι το πλήθος των
είναι το πλήθος των 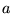 και των
και των 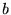 στη λέξη
στη λέξη 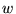 και
και 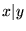 σημαίνει ότι το
σημαίνει ότι το 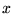 διαιρεί το
διαιρεί το 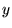 .
.
- Δείξτε ότι η γλώσσα
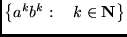 δεν είναι κανονική.
δεν είναι κανονική.
- Αν
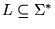 είναι μια γλώσσα η σχέση
είναι μια γλώσσα η σχέση 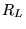 ορίζεται ως:
ορίζεται ως:
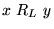 αν και μόνο αν για κάθε
αν και μόνο αν για κάθε
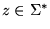 έχουμε
δηλ. τα
έχουμε
δηλ. τα 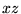 ,
, 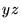 είτε ανήκουν και
τα δυο στην
είτε ανήκουν και
τα δυο στην 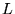 είτε κανένα.
Δείξτε ότι η σχέση
είτε κανένα.
Δείξτε ότι η σχέση 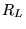 είναι σχέση ισοδυναμίας.
είναι σχέση ισοδυναμίας.
- Δώστε μια context-free γραμματική για τη γλώσσα
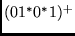 .
.
- Δείξτε ότι η γλώσσα
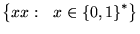 δεν είναι context free.
δεν είναι context free.
- Δείξτε ότι το σύνολο των προγραμμάτων
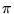 τα οποία δεν τερματίζουν δεν είναι αναδρομικά απαριθμήσιμο.
(Μπορείτε να χρησιμοποιήσετε το ότι το halting problem δεν είναι αλγοριθμικά αποφασίσιμο.)
τα οποία δεν τερματίζουν δεν είναι αναδρομικά απαριθμήσιμο.
(Μπορείτε να χρησιμοποιήσετε το ότι το halting problem δεν είναι αλγοριθμικά αποφασίσιμο.)
Mihalis Kolountzakis
2003-09-04