
Τρ, Πέ 9-11 στην Β212.
Το μεταπτυχιακό μάθημα «Πραγματική Ανάλυση» είναι μια εισαγωγή στη θεωρία ολοκλήρωσης καθώς και σε συναφείς έννοιες και αποτελέσματα της Πραγματικής και Συναρτησιακής ανάλυσης και της Θεωρίας Πιθανοτήτων. Σκοπός του μαθήματος είναι να διδάξει στο φοιτητή τις βασικές έννοιες που χρησιμοποιούνται στο χτίσιμο της θεωρίας του ολοκληρώματος αλλά και χρήση του ολοκληρώματος αυτού (ολοκλήρωμα Lebesgue) στη Μαθηματική πράξη.
Θα ακολουθήσουμε το βιβλίο του Walter Rudin, «Real and Complex Analysis, 3rd Edition».
Σε κάποιες περιπτώσεις όμως μπορεί να στηριχθούμε σε άλλα βιβλία ή σημειώσεις.
Ο βαθμός του φοιτητή θα προκύψει κατά 20% από τα σετ ασκήσεων που θα λύνει κάθε εβδομάδα, κατά 30% από το ενδιάμεσο διαγώνισμα (περί την 7η εβδομάδα του εξαμήνου) και κατά 50% από το τελικό διαγώνισμα.
Κάθε εβδομάδα, συνήθως Πέμπτη, θα σας δίνω από ένα φυλλάδιο ασκήσεων, τις λύσεις των οποίων θα πρέπει να μου επιστρέψετε μια βδομάδα μετά, στο μάθημα.
Θα πρέπει οι λύσεις που θα παραδίδετε να είναι σωστές, σύντομες (χωρίς να μακρυγορείτε αλλά και χωρίς να αφήνετε απ' έξω κάτι σημαντικό) και να είναι δικές σας. Το να παραδώσετε ασκήσεις που έχετε γράψει από άλλους δεν επιτρέπεται. Μπορείτε φυσικά να συζητάτε τα προβλήματα με άλλους αλλά η λύση που θα μου δίνετε θα πρέπει να είναι γραμμένη από σας και να έχει κατανοηθεί πλήρως από εσάς. Το να μου δίνετε ασκήσεις που δεν έχετε λύσει δε βοηθάει ούτε και μένα (γιατί δε θα καταλαβαίνω αν έχετε πρόβλημα να κατανοήσετε κάτι) αλλά ούτε και σας.
Περιοδικά θα ζητώ από κάποιους από σας να μας παρουσιάσουν τη λύση κάποιας άσκησης στο μάθημα.
Μπορείτε να τη βλέπετε εδώ
Είδαμε τι είναι μια σ-άλγεβρα πάνω σε ένα σύνολο ![]() . Σε ένα τέτοιο μετρήσιμο χώρο ορίζεται έπειτα η έννοια της μετρήσιμης
συνάρτησης
. Σε ένα τέτοιο μετρήσιμο χώρο ορίζεται έπειτα η έννοια της μετρήσιμης
συνάρτησης ![]() , όπου
, όπου ![]() είναι ένας μετρικός (ή, γενικότερα, τοπολογικός) χώρος.
Κάναμε μια πολύ σύντομη ανασκόπηση του τι είναι μετρική και μετρικός χώρος και ορίσαμε επίσης την έννοια του τοπολογικού χώρου (αν και κυρίως
θα χρησιμοποιούμε μετρικούς χώρους). Δείξαμε τέλος ότι η σύνθεση μιας συνεχούς συνάρτησης με μια μετρήσιμη συνάρτηση διατηρεί τη
μετρησιμότητα (Θεώρημα 1.7 του βιβλίου σας). Διαβάστε μόνοι σας και το Θεώρημα 1.8 που είναι πολύ παρόμοιο.
είναι ένας μετρικός (ή, γενικότερα, τοπολογικός) χώρος.
Κάναμε μια πολύ σύντομη ανασκόπηση του τι είναι μετρική και μετρικός χώρος και ορίσαμε επίσης την έννοια του τοπολογικού χώρου (αν και κυρίως
θα χρησιμοποιούμε μετρικούς χώρους). Δείξαμε τέλος ότι η σύνθεση μιας συνεχούς συνάρτησης με μια μετρήσιμη συνάρτηση διατηρεί τη
μετρησιμότητα (Θεώρημα 1.7 του βιβλίου σας). Διαβάστε μόνοι σας και το Θεώρημα 1.8 που είναι πολύ παρόμοιο.
Όσοι από εσάς έχετε ξεχάσει τα περί μετρικών χώρων ή δεν τα μάθατε ποτέ, θα πρέπει να θυμηθείτε διάφορα βασικά. Αρχίστε διαβάζοντας τις πρώτες 17 σελίδες από τις πολύ καλές σημειώσεις του συναδέλφου κ. Μήτση.
Την Πέμπτη θα πάρετε το πρώτο φυλλάδιο ασκήσεων, με παράδοση μια βδομάδα μετά.
Διατήρηση της μετρησιμότητας από αλγεβρικές πράξεις μεταξύ συναρτήσεων, όπως και από μέγιστα, ελάχιστα, sup και inf, καθώς και limsup, liminf και lim μετρησίμων συναρτήσεων.
σ-άλγεβρα που παράγεται από μια οικογένεια συνόλων. Σύνολα Borel σ' ένα τοπολογικό χώρο.
Σύνολα
![]() και παραδείγματα.
και παραδείγματα.
Οι επεκτεταμένοι πραγματικοί αριθμοί
![]() και αλγεβρικές πράξεις με τα άπειρα.
και αλγεβρικές πράξεις με τα άπειρα.
Απλές συνάρτήσεις (μη αρνητικές προς το παρόν) και θεώρημα μονότονης προσέγγισης κάθε μη αρνητικής μετρήσιμης συνάρτησης από κάτω από ακολουθία απλών συναρτήσεων.
Μη αρνητικά μέτρα και μιγαδικά μέτρα.
Σήμερα είδαμε μερικά παραδείγματα χώρων μέτρου (κυρίως το counting measure, τη μάζα Dirac) και έπειτα ορίσαμε το ολοκλήρωμα απλής μη αρνητική συνάρτηση και από αυτό τον ορισμό και το θέωρημα που δείξαμε την προηγούμενη φορά που μας επιτρέπει να προσεγγίσουμε κάθε μη αρνητική μετρήσιμη συνάρτηση από μια αύξουσα ακολουθία απλών ορίσαμε και το ολοκλήρωμα οποασδήποτε μη αρνητικής μετρήσιμης συνάρτησης. Είδαμε διάφορες ιδιότητες του ολοκληρώματος και καταλήξαμε να αποδείξουμε το θεώρημα μονότονης σύγκλισης καθώς και το πόρισμά του για την ολοκλήρωση κατά όρους σειράς μη αρνητικών συναρτήσεων. Είδαμε επίσης με ποια μεθοδολογία μπορεί κανείς να μεταγράψει κάποια θεωρήματα που αφορούν ολοκληρώματα σε αντίστοιχα θεωρήματα που αφορούν σειρές, χρησιμοποιώντας το counting measure.
Αποδείξαμε το Λήμμα του Fatou και το Θεώρημα Κυριαρχημένης Σύγκλισης (Dominated Convergence Theorem). Ορίσαμε το ολοκλήρωμα μιγαδικών (και πραγματικών) συναρτήσεων και πλέον δε μιλάμε μόνο για ολοκληρώματα μη αρνητικών συναρτήσεων. Είδαμε τις βασικές ιδιότητες του ολοκληρώματος (γραμμικότητα, τριγωνική ανισότητα). Μιλήσαμε για το τι σημαίνει για μια ιδιότητα να ισχύει «σχεδόν παντού» και το πώς μπορεί κανείς σε διάφορα θεωρήματα, όπως το Θεώρημα Κυριαρχημένης Σύγκλισης, να απαιτεί τις υποθέσεις του να ισχύουν μόνο σχεδόν παντού (και όχι κατ' ανάγκην παντού). Είδαμε ότι μια σειρά συγκλίνει σχεδόν παντού όταν η σειρά των ολοκληρωμάτων των απολύτων όρων συγκλίνει και στην περίπτωση αυτή μπορούμε να αλλάξουμε το ολοκλήρωμα με το άθροισμα.
Έχουμε ουσιαστικά τελειώσει με το Κεφάλαιο 1 του βιβλίου.
Μετά τη διόρθωση και του 2ου φυλλαδίου έχω να κάνω τα παρακάτω σχόλια και παρακαλώ πολύ να τα λάβετε υπόψιν σας.
Είδαμε κατ' αρχήν την έννοια του θετικού γραμμικού συναρτησοειδούς, παρατηρήσαμε ότι στο γραμμικό χώρο
![]() το ολοκλήρωμα Riemann
μιας συνάρτησης
το ολοκλήρωμα Riemann
μιας συνάρτησης
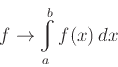
Μια συνοπτική περιγραφή του μέτρου και ολοκληρώματος Lebesgue, με έμφαση στη χρήση του και σχεδόν καθόλου στην έννοια της μετρησιμότητας, μπορείτε να βρείτε στο πρώτο κεφάλαιο του βιβλίου αυτού. Ίσως να σας φανεί χρήσιμη μαζί με τις ασκήσεις που περιέχονται εκεί.
Μιλήσαμε με λεπτομέρεια για το σύνολο του Cantor (ένα υπαριθμήσιμο σύνολο στο ![]() που έχει μέτρο Lebesgue μηδέν). Το σύνολο
Cantor (του οποίου υπάρχουν πολλές παραλλαγές) έχει πολλές ενδιαφέρουσες ιδιότητες και είναι πηγή παραδειγμάτων στην Ανάλυση.
Ρίξτε μια ματιά εδώ.
που έχει μέτρο Lebesgue μηδέν). Το σύνολο
Cantor (του οποίου υπάρχουν πολλές παραλλαγές) έχει πολλές ενδιαφέρουσες ιδιότητες και είναι πηγή παραδειγμάτων στην Ανάλυση.
Ρίξτε μια ματιά εδώ.
Αποδείξαμε ότι υπάρχουν υποσύνολα του ![]() που δεν είναι Lebesgue μετρήσιμα (§2.22 στο Rudin - δεν πήγαμε πέρα από κει στο Κεφ. 2).
που δεν είναι Lebesgue μετρήσιμα (§2.22 στο Rudin - δεν πήγαμε πέρα από κει στο Κεφ. 2).
Από το Κεφ. 3 αποδείξαμε την ανισότητα του Jensen για κυρτές συναρτήσεις (που είδαμε ότι αποτελεί κατά κάποιον τρόπο μια γενίκευση του ορισμού της κυρτότητας συνάρτησης) και αποδείξαμε επίσης και την ανισότητα του Hölder (Θ. 3.5 στο Rudin).
Δείξαμε σήμερα ξανά την ανισότητα Hölder (χρησιμοποιώντας την ανισότητα του Young:
![]() για
για ![]() και
και
![]() ).
Από την ανισότητα Hölder δείξαμε μετά την ανισότητα του Minkowski που είναι η τριγωνική
ανισότητα για τις νόρμες
).
Από την ανισότητα Hölder δείξαμε μετά την ανισότητα του Minkowski που είναι η τριγωνική
ανισότητα για τις νόρμες
![]() . Είδαμε ότι αυτές οι ανισότητες μας δίνουν (χρησιμοποιώντας
το counting measure) και τις αντίστοιχες ανισότητες για πεπερασμένα αθροίσματα και σειρές.
Αποδείξαμε ότι οι χώροι
. Είδαμε ότι αυτές οι ανισότητες μας δίνουν (χρησιμοποιώντας
το counting measure) και τις αντίστοιχες ανισότητες για πεπερασμένα αθροίσματα και σειρές.
Αποδείξαμε ότι οι χώροι ![]() είναι πλήρεις μετρικοί χώροι.
είναι πλήρεις μετρικοί χώροι.
Δείξαμε ότι σε κάθε χώρο μέτρου οι απλές συναρτήσεις είναι πυκνές στους χώρους ![]() ,
,
![]() .
(Για το χώρο
.
(Για το χώρο ![]() πρέπει κανείς να επιτρέψει και απλές συναρτήσεις στις οποίες τα σύνολα στα οποία είναι σταθερές
μπορούν να έχουν και άπειρο μέτρο. Για τους ολοκληρωτικούς χώρους
πρέπει κανείς να επιτρέψει και απλές συναρτήσεις στις οποίες τα σύνολα στα οποία είναι σταθερές
μπορούν να έχουν και άπειρο μέτρο. Για τους ολοκληρωτικούς χώρους ![]() αυτό δε χρειάζεται.)
αυτό δε χρειάζεται.)
Δείξαμε έπειτα ότι ο χώρος ![]() (συνεχείς συναρτήσεις
(συνεχείς συναρτήσεις
![]() με συμπαγή φορέα) είναι επίσης πυκνές
στους
με συμπαγή φορέα) είναι επίσης πυκνές
στους ![]() ,
,
![]() , φτάνει ο χώρος
, φτάνει ο χώρος ![]() να είναι ένας τοπικά συμπαγής μετρικός χώρος. Η πυκνότητα αυτή δεν ισχύει
για το
να είναι ένας τοπικά συμπαγής μετρικός χώρος. Η πυκνότητα αυτή δεν ισχύει
για το ![]() .
.
Χρησιμοποιώντας το προηγούμενο δείξαμε ότι οι ολοκληρωτικοί χώροι
![]() είναι διαχωρίσιμοι, ότι δηλ. έχουν
κάποιο αριθμήσιμο πυκνό υποσύνολο. Αυτό δεν ισχύει για τον
είναι διαχωρίσιμοι, ότι δηλ. έχουν
κάποιο αριθμήσιμο πυκνό υποσύνολο. Αυτό δεν ισχύει για τον
![]() και το αποδείξαμε.
και το αποδείξαμε.
Σήμερα κάναμε μια μικρή εισαγωγή στους χώρους Hilbert. Ξεκινήσαμε το Κεφ. 4 και καλύψαμε τις έννοιες μέχρι και το Θ. 4.11 (διάσπαση χώρου Hilbert στο άθροισμα ενός κλειστού υπόχωρου και του ορθογωνίου συμπληρώματός του (ορθογώνιες προβολές).
Σήμερα συνεχίσαμε να μιλάμε για χώρους Hilbert. Αποδείξαμε το θεώρημα αναπαράστασης 4.12 και μιλήσαμε μετά για ορθοκανονικά σύνολα.
Υπολογίσαμε την ορθογώνια προβολή του ![]() πάνω σε ένα υπόχωρο που παράγεται από ένα πεπερασμένο ορθοκανονικό σύνολο
πάνω σε ένα υπόχωρο που παράγεται από ένα πεπερασμένο ορθοκανονικό σύνολο
![]() ,
και είδαμε ότι οι συντελεστές της προβολής ως προς τα
,
και είδαμε ότι οι συντελεστές της προβολής ως προς τα ![]() είναι οι αριθμοί
είναι οι αριθμοί ![]() . Από αυτό αποδείξαμε την ανισότητα του Bessel
για κάθε ορθοκανονικό σύνολο. Καταλήξαμε με το Θ. 4.18 που συνοψίζει κάποιες βασικές έννοιες για ορθοκανονικά σύνολα και αναπτύγματα ως προς αυτά.
. Από αυτό αποδείξαμε την ανισότητα του Bessel
για κάθε ορθοκανονικό σύνολο. Καταλήξαμε με το Θ. 4.18 που συνοψίζει κάποιες βασικές έννοιες για ορθοκανονικά σύνολα και αναπτύγματα ως προς αυτά.
Το ενδιάμεσο διαγώνισμα θα γίνει την Πέμπτη 3-11-2016, την ώρα του μαθήματος. Να είστε στην αίθουσα ακριβώς στις 9:00 (η αίθουσα ενδέχεται να αλλάξει-θα ενημερωθείτε). Εκείνη την εβδομάδα δε θα έχετε να παραδώσετε ασκήσεις (αλλά θα παραλάβετε νέο φυλλάδιο την ημέρα του διαγωνίσματος).
Μπορείτε εδώ να δείτε ένα υπόδειγμα του διαγωνίσματος της 3-11-2016. Το διαγώνισμα θα έχει διάρκεια 2 ώρες. Θα εξεταστείτε σε 5 (μάλλον) θέματα τα οποία θα σας είναι άγνωστα χωρίς αυτό να σημαίνει ότι θα είναι και δύσκολα. Θα πάρετε και 2ο υπόδειγμα το επόμενο Σαββατοκύριακο. Δε θα έχετε να παραδώσετε φυλλάδιο ασκήσεων την εβδομάδα του ενδιάμεσου διαγωνίσματος.
Μιλήσαμε κατ' αρχήν για τους χώρους
![]() και
και
![]() (χώροι 1-περιοδικών συναρτήσεων) και για την ορθοκανονική βάση
(χώροι 1-περιοδικών συναρτήσεων) και για την ορθοκανονική βάση
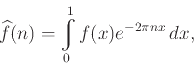
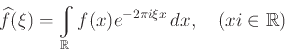
Μιλήσαμε επίσης για τον πυρήνα του Dirichlet και για τον πυρήνα του Fejer.
Αυτά που είπαμε (και που θα πούμε και την Πέμπτη) μπορείτε να τα βρείτε στα Κεφ. 2 και 3 του βιβλίου αυτού.
Συνεχίσαμε σήμερα τη συζήτηση για ανάλυση Fourier περιοδιών συναρτήσεων. Αποδείξαμε το Θεώρημα του Fejer που λέει ότι οι Cesaro μέσοι όροι των μερικών αθροισμάτων
της σειράς Fourier μια συνεχούς περιοδικής συνάρτησης συγκλίνουν ομοιόμορφα στη συνάρτηση. Αυτό έχει ως συνέπεια την πληρότητα των εκθετικών (πυκνότητα των τριγωνομετρικών
πολυωνύμων) στο χώρο ![]() .
.
Διαβάστε από εδώ.
Εδώ.
Στο μάθημα της Τρίτης θα ασχοληθούμε με λύση ασκήσεων και δε θα καλύψουμε νέα «ύλη».
Σήμερα ασχοληθήκαμε με διάφορες από τις ασκήσεις των υποδειγμάτων διαγωνίσματος.
Το διαγώνισμα θα γίνει στην Α208. Παρακαλώ να είστε εκεί στις 9:00 ακριβώς.
Αποδείξαμε σήμερα το θεώρημα του Baire και είδαμε πώς αποδεικνύεται και το θεώρημα Banach-Steinhaus (Θεώρημα Ομοιόμορφου Φράγματος).
Ως συνέπεια του θ. Banach-Steinhaus είδαμε ότι υπάρχουν συνεχείς συναρτήσεις (στο
![]() ) των οποίων η σειρά Fourier δε συγκλίνει σε ένα σημείο.
) των οποίων η σειρά Fourier δε συγκλίνει σε ένα σημείο.
Δείξαμε σήμερα το Θεώρημα Ανοιχτής Απεικόνισης και το χρησιμοποιήσαμε για να αποδείξουμε ότι υπάρχει ακολουθία ![]() ,
,
![]() , που τείνει στο 0 αλλά
δεν είναι ακολουθία συντελεστών Fourier μιας
, που τείνει στο 0 αλλά
δεν είναι ακολουθία συντελεστών Fourier μιας ![]() συνάρτησης.
συνάρτησης.
Ορίσαμε (Κεφ. 6) την έννοια του μιγαδικού μέτρου και την ολική κύμανση
![]() ενός μιγαδικού μέτρου
ενός μιγαδικού μέτρου ![]() . Δείξαμε ότι το
. Δείξαμε ότι το
![]() είναι
ένα θετικό, πεπερασμένο μέτρο. Ορίσαμε επίσης τις έννοιες της απόλυτης συνέχειας και του τι σημαίνει ένα μέτρο να είναι ιδιάζον ως προς ένα άλλο.
Αποδείξτε τις ιδιότητες που περιγράφονται στην Πρόταση 6.8 του βιβλίου ως εξάσκηση στις έννοιες αυτές.
είναι
ένα θετικό, πεπερασμένο μέτρο. Ορίσαμε επίσης τις έννοιες της απόλυτης συνέχειας και του τι σημαίνει ένα μέτρο να είναι ιδιάζον ως προς ένα άλλο.
Αποδείξτε τις ιδιότητες που περιγράφονται στην Πρόταση 6.8 του βιβλίου ως εξάσκηση στις έννοιες αυτές.
Αποδείξαμε σήμερα το θεώρημα Radon-Nikodym. Είδαμε την ανάλυση Hahn πραγματικών μέτρων. Δε συνεχίσαμε στον δυϊκό του ![]() .
.
Ορίσαμε το γινόμενο δύο σ-αλγεβρών και την έννοια του μέτρου γινόμενο και αποδείξαμε το Θεώρημα του Fubini.
Το χρησιμοποιήσαμε για να δείξουμε ότι η συνέλιξη δύο
![]() ορίζεται σχεδόν παντού και ότι
ορίζεται σχεδόν παντού και ότι
![]() .
.
Συζητήσαμε προσεκτικά τη λύση των ασκήσεων 1, 2 και 5 από το Φυλλάδιο 7.
Στο χρόνο που μας έμεινε δείξαμε την ανισότητα
![]() .
.
Είδαμε σήμερα ότι μπορεί κανείς να συμπεράνε για μια ανισότητα που αφορά νόρμες συνέλιξης το ποια ακριβώς συνθήκη
πρέπει να ικανοποιούν οι εκθέτες βάζοντας ![]() στη θέση της συνάρτησης
στη θέση της συνάρτησης ![]() για όλες τις συναρτήσεις που
συμμετέχουν στην ανισότητα. Έτσι προκύπτει μια δύναμη του
για όλες τις συναρτήσεις που
συμμετέχουν στην ανισότητα. Έτσι προκύπτει μια δύναμη του ![]() σε κάθε μεριά της ανισότητας και πρέπει οι εκθέτες
να είναι ίδιοι. Δοκιμάστε το αυτό π.χ. στην ανισότητα του Hölder
σε κάθε μεριά της ανισότητας και πρέπει οι εκθέτες
να είναι ίδιοι. Δοκιμάστε το αυτό π.χ. στην ανισότητα του Hölder
Τέλος δείξαμε την ανισότητα του Young ακολουθώντας το βιβλίο του Hörmander, The Analysis of Linear Partial Differential Operators, I, σελ. 116, Theorem 4.5.1 και Corollary 4.5.2.
Σήμερα ξεκινήσαμε το Κεφ. 7 (Differentiation) του βιβλίου που ακολουθούμε.
Την ερχόμενη εβδομάδα παρακαλώ να έρχεστε στο μάθημα με τυχόν ερωτήσεις που θα θέλατε να απαντηθούν, επί ολόκληρης της ύλης που έχουμε καλύψει αυτό το εξάμηνο. Αν είστε καλά προετοιμασμένοι και έχετε πράγματα που θέλετε να ρωτήσετε τότε θα προτιμήσω να απαντώ αυτά από το να προχωράμε πιο κάτω σε νέο υλικό.
Δώσαμε το τέλος της απόδειξης για το ότι για κάθε
![]() σχεδόν κάθε σημείο του
σχεδόν κάθε σημείο του
![]() είναι σημείο Lebesgue
της
είναι σημείο Lebesgue
της ![]() . Δε συνεχίσαμε το Κεφάλαιο από κει και πέρα. Για το υπόλοιπο της ώρας λύναμε διάφορες ασκήσεις.
. Δε συνεχίσαμε το Κεφάλαιο από κει και πέρα. Για το υπόλοιπο της ώρας λύναμε διάφορες ασκήσεις.
Σήμερα λύσαμε διάφορες ασκήσεις κατά τη διάρκεια του μαθήματος.
Για να προετοιμαστείτε για το τελικό διαγώνισμα συνιστώ παράλληλα με το διάβασμα του βιβλίου σας να λύσετε ξανά όλες τις ασκήσεις που παίρνατε εβδομαδιαία (για όλες υπάρχουν και οι λύσεις τους εδώ). Θα πρέπει να βεβαιώνεστε ότι καταλαβαίνετε τις λύσεις που διαβάζετε (το ιδανικό βέβαια είναι να μπορείτε να τις βρίσκετε ξανά μόνοι σας). Θα είμαι διαθέσιμος για να βοηθώ ολόκληρο το μήνα του Ιανουαρίου.
Καλές διακοπές και καλό διάβασμα.
Το τελικό διαγώνισμα θα γίνει την Τρίτη 31-1-2017 στη Β212 και ώρα 9:00. Η διάρκεια θα είναι σχεδόν σίγουρα πάνω από 3 ώρες, οπότε υπολογίστε ανάλογα τις υποχρεώσεις σας για μετά. Αν υπάρξει κάποια αλλαγή στην ώρα θα ανακοινωθεί εδώ.
Καλή Χρονιά σε όλους,
Θα γίνει ένα δίωρο μάθημα την Παρασκευή 27-1-2017, 10:00-12:00, στη συνηθισμένη αίθουσα B212. Σκοπός του μαθήματος αυτού είναι να έρθετε προετοιμασμένοι να ρωτήσετε πράγματα από το μάθημα που δεν έχετε καταλάβει. Αν κάποιους δεν τους βολεύει αυτή η ώρα και έχουν πράγματα να ρωτήσουν ας μου στείλουν ένα μήνυμα να συνεννοηθούμε γιατί αυτή την εβδομάδα δε θα είμαι κάθε μέρα στο γραφείο μου.
Είναι εδώ.