


Next: 5.11 Context free γραμματικές
Up: 5 Ημερολόγιο Μαθήματος (Διδακτικές
Previous: 5.9 Τρ, 5/11/02: Ελαχιστοποίηση
Contents
Δείτε εδώ για τα αποτελέσματα της προόδου (άριστα το 30).
Τα θέματα που ρωτήθηκαν ήταν τα παρακάτω 6 προβλήματα (τα πρώτα τρία για τη μισή
τάξη και τα υπόλοιπη γα την άλλη μισή).
- Κατασκευάστε DFA για τις γλώσσες (α)
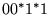 , και
(β)
, και
(β)
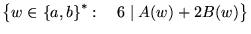 ,
όπου
,
όπου 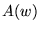 , και
, και 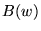 είναι το πλήθος των
είναι το πλήθος των 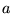 και των
και των 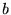 στη λέξη
στη λέξη 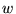 και
και 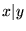 σημαίνει ότι το
σημαίνει ότι το 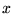 διαιρεί το
διαιρεί το 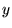 .
.
- Δώστε μια κανονική έκφραση για τη γλώσσα που αναγνωρίζει το αυτόματο
του Σχήματος 18.
Σχήμα 18. Το Σχήμα για την Άσκηση
2
- Δείξτε ότι η γλώσσα
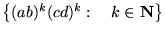 δεν είναι κανονική.
δεν είναι κανονική.
- Κατασκευάστε DFA για τις γλώσσες (α) τις λέξεις του
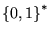 που περιέχουν την υπολέξη 0000, και
(β) τη γλώσσα που δίνεται από την κανονική έκφραση
που περιέχουν την υπολέξη 0000, και
(β) τη γλώσσα που δίνεται από την κανονική έκφραση
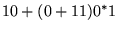 .
.
- Δώστε μια κανονική έκφραση για τη γλώσσα που αναγνωρίζει το αυτόματο
του Σχήματος 19.
Σχήμα 19. Το Σχήμα για την Άσκηση
5
- Δείξτε ότι η γλώσσα
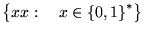 δεν είναι κανονική.
δεν είναι κανονική.
Mihalis Kolountzakis
2003-09-04