Θεωρία Προσέγγισης και Εφαρμογές

Μιχάλης Κολουντζάκης

Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών,
Πανεπιστήμιο Κρήτης,
Βούτες, 70013 Ηράκλειο, E-mail: kolount AT gmail.com

Άνοιξη 2013-14

1 Ωράριο

Τρίτη 9-11, Πέμπτη 9-11 στην αίθουσα Α208.

Ώρες γραφείου: Δευτέρα 11-1 (στο γραφείο Α305).

2 Περιγραφή του μαθήματος

Δίδαξα το ίδιο μάθημα την Άνοιξη του 2010-11 και μπορείτε να δείτε την ιστοσελίδα αυτού του μαθήματος για να προσανατολιστείτε για το περιεχόμενο.

2.1 Σημειώσεις μαθήματος

Εκεί μπορείτε να δείτε και τις σημειώσεις του μαθήματος για εκείνο το εξάμηνο. Οι σημειώσεις αυτές θα αποτελέσουν τη βάση και για τις σημειώσεις που θα παίρνετε κατά τη διάρκεια του μαθήματος.

Όπως και το 2010-11 το μάθημα και οι σημειώσεις θα βασιστούν αρκετά στις σημειώσεις του N. L. Carothers, "A Short Course on Approximation Theory", που βρίσκονται εδώ σε μορφή PDF.

Οι σημειώσεις του μαθήματος που γράφονται αυτό το εξάμηνο θα εμφανίζονται

εδώ

(τελυταία ενημέρωση: Δευτέρα 19/5/2014).

3 Βαθμολογικό Σύστημα - Εξετάσεις

Στο μάθημα θα υπάρχουν τρία υποχρεωτικά διαγωνίσματα. Τα δύο από αυτά θα γίνουν περίπου στο 1/3 και 2/3 του μαθήματος και το τελευταίο θα γίνει την τελευταία εβδομάδα των μαθημάτων.

Κάθε ένα από αυτά τα διαγωνίσματα θα μετράει κατά το 1/3 του βαθμού.

Διαγώνισμα	Ημερομηνία
1ο	Πέμπτη 20 Μαρτίου 2014
2ο	Τρίτη 6 Μαϊου 2014
3ο	Πέμπτη 29 Μαϊου 2014

Τα διαγωνίσματα θα γίνουν στη διάρκεια του δίωρου του μαθήματος.

3.1 Εξαίρεση από τα υποχρεωτικά διαγωνίσματα

Αν κάποιος έχει κάποιο σοβαρό λόγο να μη μπορεί να δώσει τα υποχρεωτικά διαγωνίσματα τότε μπορεί, εγγράφως (στέλνοντας μου email) να εξηγήσει το γιατί δεν μπορεί να εξεταστεί στα τρία αυτά διαγωνίσματα και να επιλέξει να εξεταστεί στο τελικό διαγώνισμα. Αυτό θα πρέπει να γίνει έως τις 10 Μαρτίου 2014. Όποιος δεν έχει επιλέξει το τελικό διαγώνισμα μέχρι τότε θεωρείται ότι θα δώσει τα τρία διαγωνίσματα.

Τονίζω εδώ ότι ή τα τρία διαγωνίσματα δίνει κάποιος ή το τελικό διαγώνισμα. Δε μπορεί να δώσει και τα δύο. Το τελικό διαγώνισμα θα είναι επί όλης της διδαχθείσας ύλης του μαθήματος ενώ τα τρία διαγωνίσματα θα είναι, το καθένα, κυρίως επί του αντίστοιχου κομματιού του μαθήματος.

ΑΝΑΚΟΙΝΩΣΗ (13/5/2014): Όσοι φοιτητές είχαν επιλέξει να εξεταστούν μόνο σε τελικό διαγώνισμα θα πρέπει να επικονωνήσουν μαζί μου για να εξεταστούν προφορικά.

4 Ημερολόγιο Μαθήματος

4.1 Τρ, 18/2/2014

Μιλήσαμε λίγο για την έννοια της μετρικής (απόστασης) που μπορεί να οριστεί σε ένα σύνολο. Είδαμε τα αξιώματα που πρέπει να πληροί η μετρική και είδαμε επίσης και μερικά παραδείγματα. Έπειτα αναφερθήκαμε στην έννοια του γραμικού χώρου (διανυσματικού χώρου) με συντελεστές από το ${\mathbb{R}}$ ή το ${\mathbb{C}}$ . Αναφερθήκαμε λίγο στα δύο βασικά παραδείγματα τέτοιων γραμμικών χώρων, το ${\mathbb{R}}^n$ και το ${\mathbb{C}}^n$ , και μιλήσαμε για την έννοια της γραμμικής ανεξαρτησίας και την έννοια της διάστασης. Είδαμε ότι αυτές οι έννοιες εξαρτώνται από το αν δουλεύουμε με το ${\mathbb{R}}$ ή το ${\mathbb{C}}$ .

Αρχίσαμε τέλος να αναφερουμε διάφορα παραδείγματα γραμμικών χώρων συναρτήσεων, όπως τους χώρους

: συνεχείς συναρτήσεις στο διάστημα (είδαμε μάλιστα ότι ο γραμμικός αυτός χώρος είναι απειροδιάσταστος δίνοντας, για κάθε , ένα παράδειγμα συναρτησεων $f_1,\ldots,f_n \in C([a,b])$ που είναι γραμμικώς ανεξάρτητες.
: συναρτήσεις που είναι φορές συνεχώς παραγωγίσιμες στο διάστημα .
$C^\infty((a,b))$ : ομαλές συναρτήσεις, συναρτήσεις δηλ. που έχουν άπειρες παραγώγους.
$C_c({\mathbb{R}})$ : συνεχείς συναρτήσεις επί του ${\mathbb{R}}$ με συμπαγή φορέα. Αυτό σημαίνει ότι κάθε τέτοια συνάρτηση είναι 0 εκτός κάποιου διαστήματος (το διάστημα αυτό εξαρτάται από τη συνάρτηση).

4.2 Πέ, 20/2/2014

Είδαμε ξανά διάφορα παραδείγματα γραμμικών χώρων όπως και μερικά νέα:

$C_b({\mathbb{R}})$ : οι φραγμένες συναρτήσεις ${\mathbb{R}}\to{\mathbb{C}}$ .
${\mathcal P}_n$ και ${\mathcal P}$ : Ο χώρος των (αλγεβρικών) πολυωνύμων βαθμού $\le n$ :

$\begin{displaymath} p(x) = p_0 + p_1 x+ p_2 x^2 + \cdots + p_n x^n, (p_j \in {\mathbb{C}}), \end{displaymath}$

και ο χώρος όλων των πολυωνύμων, ανεξαρτήτως βαθμού,

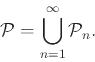
$\begin{displaymath} {\mathcal P} = \bigcup_{n=1}^\infty {\mathcal P}_n. \end{displaymath}$
${\mathcal T}_N$ : ο χώρος όλων των τριγονωμετρικών πολυωνύμων βαθμού μέχρι :

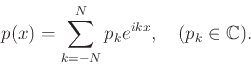
$\begin{displaymath} p(x) = \sum_{k=-N}^N p_k e^{ikx}, (p_k \in {\mathbb{C}}). \end{displaymath}$

Είδαμε επίσης την έννοια της περιοδικής συνάρτησης καθώς και το ότι το σύνολο των περιόδων μιας συνάρτησης ορισμένης πάνω στο ${\mathbb{R}}$ είναι μια προσθετική υποομάδα του ${\mathbb{R}}$ .

Ορίσαμε την έννοια της νόρμας πάνω σε ένα γραμμικό χώρο και είδαμε ότι κάθε νόρμα ορίζει μια μετρική. Είδαμε τα εξής δύο παραδείγματα νορμών πάνω στο χώρο ${\mathbb{C}}^n$ :

${\left\Vert{z}\right\Vert}_1 = {\left\vert{z_1}\right\vert}+\cdots_{\left\vert{z_n}\right\vert}$ , όπου $z = (z_1, \ldots, z_n)$ ,
${\left\Vert{z}\right\Vert}_\infty = \max{\left\{{{\left\vert{z_1}\right\vert},\ldots,{\left\vert{z_n}\right\vert}}\right\}}$ .

4.2.1 Φυλλάδιο ασκήσεων Νο 1

Βρίσκεται εδώ σε μορφή PDF.

4.3 Τρ, 25/2/2014: Παραδείγματα νορμών. Κυρτά σύνολα. Ομοιόμορφη σύγκλιση.

Είδαμε επιπλέον παραδείγματα διανυσματικών χώρων με νόρμες. Συγκεκριμένα είδαμε το πώς ορίζονται οι νόρμες ${\left\Vert{\cdot}\right\Vert}_\infty, {\left\Vert{\cdot}\right\Vert}_1$ και ${\left\Vert{\cdot}\right\Vert}_2$ στο γραμμικό χώρο και σε υπόχωρους του ${\mathbb{C}}^\infty$ , του γραμμικού χώρου όλων των μιγαδικών ακολουθιών

$\begin{displaymath} z = (z_1, z_2, \ldots). \end{displaymath}$

Για τη ${\left\Vert{\cdot}\right\Vert}_2$ δεν αποδείξαμε την τριγωνική ανισότητα (θα το κάνουμε αργότερα).

Ορίσαμε την έννοια του κυρτού συνόλου όπως και την έννοια του κυρτού συνδυασμού διανυσμάτων και αποδείξαμε ότι η μοναδιαία κλειστή μπάλα (ομοίως και η ανοιχτή μπάλα που ορίζεται ομοίως αλλά με αυστηρή ανισότητα) ενός χώρου με νόρμα

$\begin{displaymath} B = {\left\{{v\in V: {\left\Vert{x}\right\Vert} \le 1}\right\}} \end{displaymath}$

είναι κυρτό σύνολο.

Επαναλάβαμε την έννοια της ομοιόμορφης σύγκλισης και είδαμε ότι ένας πολύ διαισθητικός τρόπος να διατυπώσουμε το ότι $f_n \to f$ ομοιόμορφα είναι να πούμε ότι ${\left\Vert{f_n-f}\right\Vert}_\infty \to 0$ .

4.4 Πέ, 27/2/2014: Εσωτερικό γινόμενο και ιδιότητες. Ισοδυναμίες νορμών.

Είδαμε σήμερα το πώς ορίζεται το εσωτερικό γινόμενο δύο διανυσμάτων $z, w \in {\mathbb{C}}^n$ ή δύο συναρτήσεων $f, g \in C([a,b])$ :

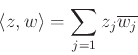
$\begin{displaymath} {\langle z, w \rangle} = \sum_{j=1} z_j \overline{w_j} \end{displaymath}$

και

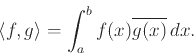
$\begin{displaymath} {\langle f, g \rangle} = \int_a^b f(x) \overline{g(x)} dx. \end{displaymath}$

Είδαμε τις διάφορες αλγεβρικές ιδιότητες του εσωτερικού γινομένου και κάναμε την παρατήρηση ότι

$\begin{displaymath} {\left\Vert{z}\right\Vert}_2^2 = {\langle z, z \rangle} \end{displaymath}$

(1)

και στο ${\mathbb{C}}^n$ και στο

. Είδαμε πως αυτή η ιδιότητα κάνει τον υπολογισμό της $\ell^2$ νόρμας πολύ εύκολη.

Αποδείξαμε την ανισότητα Cauchy - Schwartz

$\begin{displaymath} {\left\vert{{\langle z, w \rangle}}\right\vert} \le {\left\Vert{z}\right\Vert}_2 {\left\Vert{w}\right\Vert}_2 \end{displaymath}$

(η οποία ισχύει σε όποιο χώρο έχουμε ορίσει το εσωτερικό γινόμενο και την αντίστοιχη νόρμα που ορίζεται μέσω του εσωτερικού γινομένου από την (1)) και είδαμε ότι συνέπειά της είναι η τριγωνική ανισότητα για την $\ell^2$ νόρμα (που δεν την είχαμε αποδείξει μέχρι τώρα).

Ορίσαμε το τι σημαίνει για δύο νόρμες πάνω στον ίδιο γραμμικό χώρο να είναι ισοδύναμες. Αποδείξαμε έπειτα ότι από τις νόρμες

$\begin{displaymath} {\left\Vert{\cdot}\right\Vert}_\infty, {\left\Vert{\cdot}\right\Vert}_1, {\left\Vert{\cdot}\right\Vert}_2 \end{displaymath}$

στο γραμμικό χώρο συναρτήσεων

κανένα ζεύγος δεν αποτελείται από ισοδύναμες νόρμες.

4.4.1 Φυλλάδιο ασκήσεων Νο 2

Βρίσκεται εδώ σε μορφή PDF.

4.5 Τρ, 4/3/2014: Μια μικρή εισαγωγή στους μετρικούς χώρους

Με αφορμή την έννοια της ισοδυναμίας νορμών και το γεγονός ότι αν έχουμε δύο ισοδύναμες νόρμες ${\left\Vert{\cdot}\right\Vert}_a, {\left\Vert{\cdot}\right\Vert}_b$ στο γραμμικό χώρο τότε αν μια ακολουθία στοιχείων του συγκλίνει στο $x\in V$ ως προς τη νόρμα ${\left\Vert{\cdot}\right\Vert}_a$ (αυτό σημαίνει ${\left\Vert{x_n - x}\right\Vert}_a \to 0$ ) τότε συγκλίνει και ως προς τη νόρμα ${\left\Vert{\cdot}\right\Vert}_b$ (δηλ. ${\left\Vert{x_n-x}\right\Vert}_b \to 0$ ), κάναμε μια μικρή εισαγωγή στην έννοια του μετρικού χώρου, στο τι σημαίνει σύγκλιση μιας ακολουθίας σε ένα μετρικό χώρο, τι σημαίνει συνέχεια μιας συνάρτησης από ένα μετρικό χώρο σε ένα άλλο, τι είναι ανοιχτό σύνολο και τι είναι κλειστό σύνολο. Αυτές είναι πολύ θεμελιώδεις έννοιες και θα τις βρίσκουμε συνεχώς μπροστά μας με τη μια μορφή ή την άλλη. Δώσαμε αρκετά παραδείγματα και αποδείξαμε και κάποια βασικά πράγματα όπως το ότι μια οποιαδήποτε ένωση ανοιχτών συνόλων είναι ανοιχτό και ότι μια οποιαδήποτε τομή κλειστών συνόλων είναι κλειστό. Είδαμε ότι μια οποιαδήποτε τομή ανοιχτών δεν είναι αναγκαστικά ανοιχτό, μια οποιαδήποτε ένωση κλειστών δεν είναι αναγκαστικά κλειστό αλλά αν περιοριστούμε σε τομή πεπερασμένου πλήθους ανοιχτών και σε ένωση πεπερασμένου πλήθους κλειστών τότε το αποτέλεσμα είναι, αντίστοιχα, ανοιχτό και κλειστό σύνολο. Ισχύει επίσης το πολύ βασικό ότι ένα σύνολο είναι ανοιχτό αν και μόνο αν το συμπλήρωμά του είναι κλειστό αλλά αυτό δεν το αποδείξαμε (αποδείξτε το μόνοι σας, είναι εύκολο).

Σας συνιστώ να διαβάσετε σχετικά τις πρώτες 17 σελίδες από τις πολύ ωραίες σημειώσεις του κυρίου Μήτση..

4.6 Πέ, 6/3/2014: Βέλτιστη προσέγγιση από υπόχωρο πεπερασμένης διάστασης

Συμπληρώσαμε στην αρχή τη συζήτηση του προηγούμενου μαθήματος για μετρικούς χώρους με την έννοια της συμπάγειας. Ένα σύνολο το λέμε συμπαγές αν κάθε ακολουθία $x_n \in K$ έχει υπακολουθία που συγκλίνει σε κάποιο στοιχείο του . Αν ο μετρικός μας χώρος είναι ένας γραμμικός χώρος με νόρμα, πεπερασμένης διάστασης (αυτό είναι σημαντικό), τότε τα συμπαγή σύνολα είναι ακριβώς τα κλειστά και φραγμένα (φραγμένο λέγεται ενα σύνολο αν περιέχεται σε κάποια μπάλα του μετρικού χώρου). Αυτό είναι το θεώρημα Heine-Borel το οποίο δεν το αποδείξαμε.

Δείξαμε έπειτα ότι σε γραμμικό χώρο πεπερασμένης διάστασης οποιεσδήποτε δύο νόρμες είναι ισοδύναμες. Αυτό είναι πολύ σημαντικό γιατί σημαίνει ότι αν αλλάξουμε νόρμα σε ένα τέτοιο χώρο τότε η έννοια της σύγκλισης δεν αλλάζει, αφού εύκολα βλέπουμε από τον ορισμό της ισοδυναμίας νορμών ότι αν $x_n \to x$ ως προς τη μία νόρμα τότε το ίδιο ισχύει και ως προς την άλλη. Επίσης δεν αλλάζουν τα ανοιχτά και τα κλειστά σύνολα, οι συνεχείς συναρτήσεις που είναι ορισμένες πάνω στο χώρο ή παίρνουν τιμές στο χώρο, δεν αλλάζει όπως λέμε η τοπολογία του χώρου. Μπορούμε να μιλάμε γι' αυτές τις έννοιες χωρίς να προσδιορίζουμε για ποια νόρμα μιλάμε. Αλλά μόνο για χώρους με πεπερασμένη διάσταση.

Πόρισμα αυτού είναι ότι όλοι οι χώροι πεπερασμένης διάστασης είναι πλήρεις (ένας μετρικός χώρος λέγεται πλήρης αν κάθε ακολουθία που είναι Cauchy έχει όριο στο χώρο μας) και επίσης ότι κάθε κλειστή μπάλα $B_r(x) = {\left\{{y: {\left\Vert{x-y}\right\Vert} \le r}\right\}}$ σε χώρο πεπερασμένης διάστασης είναι συμπαγές σύνολο.

Δείξαμε έπειτα ότι αν είναι ένας γραμμικός χώρος με νόρμα και $Y \subseteq X$ είναι ένας γραμμικός υπόχωρος πεπερασμένης διάστασης τότε πάντα υπάρχει βέλτιστη προσέγγιση των στοιχείων του από στοιχεία του . Δηλ. για κάθε $x \in X$ υπάρχει $x^* \in Y$ τέτοιο ώστε

$\begin{displaymath} {\left\Vert{x-x^*}\right\Vert} \le {\left\Vert{x-y}\right\Vert} \forall y \in Y. \end{displaymath}$

Αν ο χώρος

δεν είναι πεπερασμένης διάστασης τότε αυτή η βέλτιστη προσέγγιση μπορεί να μην υπάρχει. Μπορεί δηλ. το $\inf_{y\in Y}{\left\Vert{x-y}\right\Vert}$ να μη «πιάνεται» για κανένα $y \in Y$ (είδαμε ένα τέτοιο παράδειγμα). Τέλος είδαμε ότι αν ο υπόχωρος πεπερασμένης διάστασης

είναι τέτοιος ώστε η βέλτιστη προσέγγιση να είναι μοναδική τότε η απεικόνιση $x \to x^*$ που στέλνει κάθε σημείο του

στο πλησιέστερό του σημείο στον

είναι συνεχής απεικόνιση (δηλ. αν $x_n \to x$ τότε έπεται $x_n^* \to x^*$ ).

4.6.1 Φυλλάδιο ασκήσεων Νο 3

Βρίσκεται εδώ σε μορφή PDF.

4.7 Τρ, 11/3/2014: Απόδειξη του θ. Weierstrass

Ξεκινήσαμε σήμερα την απόδειξη του θ. του Weierstrass, που λέει ότι κάθε συνάρτηση $f \in C([a,b])$ μπορεί να προσεγγιστεί ομοιόμορφα (δηλ. στην νόρμα ${\left\Vert{\cdot}\right\Vert}_\infty$ ) από μια ακολουθία πολυωνύμων. Δείξαμε κατ' αρχήν ότι το θεώρημα δεν ισχύει αν το διάστημα δεν είναι κλειστό (είναι π.χ. το ) ή δεν είναι φραγμένο (π.χ. το $[a,+\infty)$ ). (Για το πρώτο ένα αντιπαράδειγμα είναι η συνάρτηση στο διάστημα και για το δεύτερο ένα αντιπαράδειγμα είναι η συνάρτηση στο διάστημα $[0,+\infty)$ . Βεβαιωθείτε ότι καταλαβαίνετε γιατί αυτές οι δύο συναρτήσεις δε μπορούν να προσεγγιστούν ομοιόμορφα από ακολουθία πολυωνύμων στα αντίστοιχα διαστήματα.)

Έπειτα δείξαμε (α) ότι αρκεί να αποδείξουμε το θεώρημα στην ειδική περίπτωση που το διάστημα είναι αυτό που εμείς προτιμάμε, για παράδειγμα, στο διάστημα . Αυτό συμβαίνει επειδή για κάθε άλλο διάστημα υπάρχει μια πολυωνυμική απεικόνιση

$\begin{displaymath} \phi: [0,1] \to [a,b] \end{displaymath}$

που δίνεται από τον τύπο

$\begin{displaymath} \phi(x) = a+x(b-a) \end{displaymath}$

η οποία είναι 1-1 και επί και επίσης η αντίστροφή της είναι κι αυτή μια πολυωνυμική απεικόνιση

$\begin{displaymath} \phi^{-1}(x) = \frac{x-a}{b-a}. \end{displaymath}$

Αυτό σημαίνει ότι αν

είναι πολυώνυμο που το κοιτάμε πάνω στο διάστημα

τότε το $P(x) = p(\phi^{-1}(x))$ , που είναι μια συνάρτηση ορισμένη πάνω στο

, είναι επίσης πολυώνυμο. Έτσι το να μπορούμε να προσεγγίσουμε με πολυώνυμα συνεχείς συναρτήσεις επί του

συνεπάγεται ότι μπορούμε να προσεγγίσουμε με πολυώνυμα συνεχείς συναρτήσεις επί του

(και πάλι, βεβαιωθείτε ότι καταλαβαίνετε ακριβώς το μηχανισμό με τον οποίο μεταφέρεται η ισχύς του θεωρήματος από το

στο

Η επόμενη απλούστευση είναι ότι μπορούμε να υποθέσουμε ότι η συνάρτηση $f \in C([0,1])$ ικανοποιεί τις συνθήκες

$\begin{displaymath} f(0) = f(1) = 0. \end{displaymath}$

Ο λόγος που μπορούμε να το υποθέσουμε αυτό είναι ότι μπορούμε να αφαιρέσουμε από την

μια συνάρτηση της μορφής

που έχει τις ίδιες τιμές με την

στα άκρα του διαστήματος. Οποιαδήποτε πολυωνυμική προσέγγιση για τη νέα αυτή συνάρτηση μπορεί να μετατραπεί σε μια εξίσου καλή πολυωνυμική συνάρτηση για την

απλά προσθέτοντάς της την συνάρτηση

. Έτσι παραμένει φυσικά πολυωνυμική συνάρτηση.

Πριν συνεχίσουμε την απόδειξη του θεωρήματος του Weierstrass σε αυτή την περίπτωση (δηλ. $f \in C([0,1])$ με ) ορίσαμε τη συνέλιξη δύο συναρτήσεων $f, g: {\mathbb{R}}\to{\mathbb{C}}$

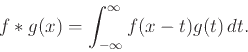
$\begin{displaymath} f*g(x) = \int_{-\infty}^{\infty} f(x-t)g(t) dt. \end{displaymath}$

Για να έχει νόημα αυτό το ολοκλήρωμα υποθέτουμε (α) ότι οι

είναι τμηματικά συνεχείς και (β) ότι τουλάχιστον μία από τις δύο έχει φραγμένο φορέα. Μια συνάρτηση έχει φραγμένο φορέα αν μηδενίζεται έξω από κάποιο (φραγμένο) διάστημα. Δείξαμε ότι

με μια απλή αλλαγή μεταβλητής και επίσης δείξαμε ότι αν

είναι ένα πολυώνυμο και

είναι τμηματικά συνεχής με φραγμένο φορέα τότε και η συνάρτηση

είναι επίσης πολυώνυμο, βαθμού όχι μεγαλύτερου από το βαθμό του

4.8 Πέ, 13/3/2014: Συμπλήρωση της απόδειξης του θ. Weierstrass

Ορίσαμε σήμερα την έννοια της προσέγγισης της μονάδας. Μια ακολουθία συναρτήσεων $\phi_n:{\mathbb{R}}\to{\mathbb{R}}$ ονομάζεται προσέγγιση της μονάδας αν ισχύουν τα παρακάτω:

Οι $\phi_n$ είναι τμηματικά συνεχείς (και απλά Riemann ολοκληρώσιμες σε κάθε διάστημα είναι αρκετό).
$\phi_n(x) \ge 0$ για κάθε $x \in {\mathbb{R}}$ , και κάθε .
$\int_{-\infty}^{+\infty} \phi_n(x) dx = 1$ για κάθε .
Για κάθε $\delta>0$ ισχύει

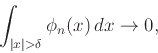
$\begin{displaymath} \int_{{\left\vert{x}\right\vert}>\delta} \phi_n(x) dx \to 0, \end{displaymath}$

όπου χρησιμοποιήσαμε το συμβολισμό $\int_{{\left\vert{x}\right\vert}>\delta} = \int_{-\infty}^{-\delta} + \int_\delta^\infty$ .

Έπειτα δείξαμε το πολύ βασικό θεώρημα προσέγγισης ότι αν $f:{\mathbb{R}}\to{\mathbb{C}}$ είναι συνεχής παντού και με φραγμένο φορέα και $\phi_n$ είναι μια προσέγγιση της μονάδας τότε ${\left\Vert{f-f*\phi_n}\right\Vert}_\infty \to 0$ , συγκλίνει δηλ. η ακολουθία συναρτήσεων $f*\phi_n$ στην

ομοιόμορφα στο ${\mathbb{R}}$ .

Ας είναι τώρα $f:{\mathbb{R}}\to{\mathbb{C}}$ μια συνεχής συνάρτηση με φορέα στο . Ορίζουμε τις συναρτήσεις

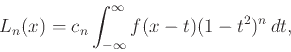
$\begin{displaymath} L_n(x) = c_n \int_{-\infty}^{\infty} f(x-t)(1-t^2)^n dt, \end{displaymath}$

όπου οι σταθερές

ορίζονται από την απαίτηση να ισχύει

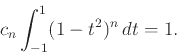
$\begin{displaymath} c_n \int_{-1}^1 (1-t^2)^n dt = 1. \end{displaymath}$

Αποδείξαμε έπειτα ότι αν

είναι το πολυώνυμο

τότε ισχύει

$\begin{displaymath} L_n(x) = f*g_n(x), \forall x \in [0,1]. \end{displaymath}$

Άρα η συνάρτηση

ισούται με πολυώνυμο στο διάστημα

(αφού έχουμε δείξει ότι συνέλιξη συνάρτησης με πολυώνυμο είναι πολυώνυμο). Η απόδειξη του θεωρήματος Weierstrass συμπληρώνεται αφού αποδείξουμε ότι η συνάρτηση

$\begin{displaymath} \phi_n(x) = g_n(x) \cdot {\bf 1}\left({\left\vert{x}\right\vert}\le 1\right) \end{displaymath}$

είναι προσέγγιση της μονάδας (χρησιμοποιήσαμε το συμβολισμό ${\bf 1}\left(\cdots\right)$ για να συμβολίσουμε το 1 αν ισχύει η συνθήκη που είναι μέσα στο ${\bf 1}\left(\cdot\right)$ και 0 αν δεν ισχύει.

ΑΝΑΚΟΙΝΩΣΗ: Την επόμενη Τρίτη 18/3 θα λύσουμε ασκήσεις και απορίες στο μάθημα. Ελάτε προετοιμασμένοι να ρωτάτε για τα πράγματα που δεν έχετε καταλάβει.

4.8.1 Φυλλάδιο ασκήσεων Νο 4

Βρίσκεται εδώ σε μορφή PDF.

4.9 Τρ, 18/3/2014: Λύση ασκήσεων

Σήμερα λύσαμε διάφορες ασκήσεις από τα 4 πρώτα φυλλάδια ασκήσεων.

4.10 Πέ, 20/3/2014: Πρώτο διαγώνισμα

Βρίσκεται εδώ σε μορφή PDF μαζί με τις λύσεις.

4.10.1 Βαθμοί 1ου Διαγωνίσματος

Εδώ σε μορφή PDF.

4.10.2 Απολογισμός 1ου Διαγωνίσματος

Με βάση τις απαντήσεις που δώσατε στα προβλήματα του διαγωνίσματος πιστεύω ότι είναι εξαιρετικά σημαντικό, ειδικά για όσους πήραν βαθμολογία από 50 και κάτω, να πάρετε υπόψιν σας τις παρακάτω παρατηρήσεις μου και να δουλέψετε πιο εντατικά.

Δεν έχετε ακόμη κατανοήσει την έννοια του γραμμικού χώρου, ειδικά όταν τα στοιχεία του γραμμικού χώρου είναι συναρτήσεις και όχι «διανύσματα» με μερικές θέσεις αριθμών το καθένα.
Λύστε π.χ. τις ασκήσεις που εμφανίζονται εδώ.
Δεν είστε αρκετά εξοικειωμένοι με τους μιγαδικούς αριθμούς και ειδικά με τις συναρτήσεις που παίρνουν μιγαδικές τιμές. Π.χ. πολλοί από σας δε μιλάνε κατ' ευθείαν για πολυώνυμο με μιγαδικούς συντελεστές αλλά το βλέπουν ως ένα αντικείμενο της μορφής όπου τα είναι πολυώνυμα με πραγματικούς συντελεστές.
Λύστε μερικές ασκήσεις από τις 4 πρώτες ομάδες εδώ.
Δεν ξέρετε πώς να αποδείξετε μια ανισότητα. Σε πολλές περιπτώσεις φτάνατε μετά από αλγεβρικούς μετασχηματισμούς σε μια ανισότητα (την οποία πρέπει να αποδείξετε ώστε να αποδειχτεί μέσω αυτής και η αρχική σας ανισότητα) και απλά λέγατε ότι ισχύει σαν να ήταν προφανής, ενώ σε καμία περίπτωση δεν ήταν και ήθελε κι άλλη δουλειά.
Το κείμενο αυτό είναι πολύ καλό. Κάποιες από τις ανισότητες που έχει μέσα δεν τις έχουμε κάνει στο μάθημα αλλά πιθανόν να τις έχετε δει σε άλλα μαθήματα. Διαβάστε το και συμπληρώστε τις αποδείξεις που λείπουν με τις υποδείξεις που δίνονται.

4.11 Τρ, 25/3/2014: Αργία, δεν έγινε μάθημα.

Σήμερα δεν έγινε μάθημα λόγω αργίας.

4.12 Πέ, 27/3/2014: Μέτρο συνέχειας συνάρτησης και ποσοτική εκτίμηση του σφάλματος προσέγγισης

Αναφέραμε καταρχήν σήμερα τα πολυώνυμα Bernstein μιας συνεχούς συνάρτησης $f \in C([0,1])$ . Αναφέραμε ότι τα πολυώνυμα αυτά συγκλίνουν στην $\infty$ νόρμα (ομοιόμορφα δηλ.) στην αλλά δεν το αποδείξαμε. Η απόδειξη βρίσκεται στις σημειώσεις που θα βρείτε στην κορυφή αυτής της σελίδας. Αποτελεί μια εναλλακτική απόδειξη του θεωρήματος του Weierstrass.

Έπειτα ορίσαμε την έννοια του μέτρου συνέχειας μιας συνάρτησης $f:K\to{\mathbb{C}}$ που είναι μια συνάρτηση $\omega_f:(0,\infty) \to [0,\infty]$ (μπορεί να πάρει και την τιμή $+\infty$ ) που ορίζεται από τον τύπο

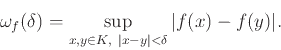
$\begin{displaymath} \omega_f(\delta) = \sup_{x,y \in K, {\left\vert{x-y}\right\vert}<\delta} {\left\vert{f(x)-f(y)}\right\vert}. \end{displaymath}$

Με άλλα λόγια αν τα

απέχουν το πολύ $\delta$ τότε τα

απέχουν το πολύ $\omega_f(\delta)$ . Το μέτρο συνέχειας είναι ένας τρόπος ποσοτικοποίησης του «πόσο συνεχής είναι μια συνάρτηση».

Υπολογίσαμε το μέτρο συνέχειας διαφόρων συναρτήσεων σε διάφορα πεδία ορισμού και αποδείξαμε ότι για μια συνάρτηση ισχύει $\lim_{\delta \to 0^+} \omega_f(\delta) = 0$ αν και μόνο αν η συνάρτηση είναι ομοιόμορφα συνεχής στο πεδίο ορισμού της.

Τέλος αναφέραμε χωρίς απόδειξη (μπορείτε να βρείτε την αποδειξη στις σημειώσεις) ότι αν $f \in C([0,1])$ και είναι το -οστό πολυώνυμο Bernstein της τότε ισχύει η ανισότητα

$\begin{displaymath} {\left\Vert{f - B_n(f)}\right\Vert}_\infty \le 2 \omega_f(1/\sqrt{n}). \end{displaymath}$

Αυτό αποτελεί μια ποσοτική μορφή του θεωρήματος Weierstrass μια και $\omega_f(1/\sqrt{n}) \to 0$ αφού η

είναι και ομοιόμορφα συνεχής (ως συνεχής σε κλειστο φραγμένο διάστημα).

4.12.1 Φυλλάδιο ασκήσεων Νο 5

Βρίσκεται εδώ σε μορφή PDF.

4.13 Τρ, 1/4/2014: Τριγωνομετρικά πολυώνυμα. Περιοδικές συναρτήσεις.

Θυμηθήκαμε τον ορισμό ου τριγωνομετρικού πολυωνύμου και αποδείξαμε κατ' αρχήν ότι κάθε τριγωνομετρικό πολυώνυμο, ως συνάρτηση, καθορίζει τους συντελεστές του. Αν δηλ. δύο τριγωνομετρικά πολυώνυμα είναι ίσα ως συναρτήσεις παντού

$\begin{displaymath} \sum_{k=-M}^M p_k e^{i k x} = \sum_{j=-N}^N r_j e^{ijx}, \forall x \in [0,2\pi) \end{displaymath}$

τότε έχουν τους ίδιους συντελεστές, δηλ.

και

για κάθε $k=-N,\ldots,N$ . Για να αποδείξουμε το θέωρημα αυτό της μοναδικότητας χρειάστηκε να υπολογίσουμε τη λεγόμενη ορίζουσα Vandermonde.

Μιλήσαμε έπειτα για περιοδικές συναρτήσεις στο ${\mathbb{R}}$ , είδαμε ότι το σύνολο των περιόδων μιας συνάρτησης είναι μια προσθετική υποομάδα του ${\mathbb{R}}$ και ότι αν η συνάρτηση είναι συνεχής και όχι σταθερή τότε η υποομάδα αυτή είναι απλά τα ακέραια πολλαπλάσια ενός θετικού αριθμού που ονομάζεται ελάχιστη περίοδος της συνάρτησης.

Δείξαμε έπειτα ότι αν μια συνάρτηση είναι -περιοδική τότε το ολοκλήρωμά της σε οποιοδήποτε διάστημα μήκους πάνω στην πραγματική ευθεία είναι το ίδιο.

Ορίσαμε το εσωτερικό γινόμενο και τη 2-νόρμα στο διάστημα $[0,2\pi]$

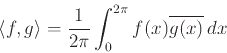
$\begin{displaymath} {\langle f, g \rangle} = \frac{1}{2\pi}\int_0^{2\pi} f(x)\overline{g(x)} dx \end{displaymath}$

και

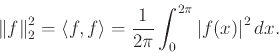
$\begin{displaymath} {\left\Vert{f}\right\Vert}_2^2 = {\langle f, f \rangle} = \frac{1}{2\pi}\int_0^{2\pi} {\left\vert{f(x)}\right\vert}^2 dx. \end{displaymath}$

Δείξαμε ότι για κάθε τριγωνομετρικό πολυώνυμο $p(x) = \sum_{k=-N}^N p_k e^{ikx}$ ισχύει $p_k = {\langle p, e^{ikx} \rangle}$ λόγω του ότι οι συναρτήσεις $e^{ikx}$ για διαφορετικές ακέραιες τιμές του αποτελούν ένα ορθοκανονικό σύστημα (είναι δηλ. ανά δύο ορθογώνιες και κάθε μια τους έχει 2-νόρμα ίση με 1). Τέλος αποδείξαμε τον τύπο

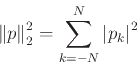
$\begin{displaymath} {\left\Vert{p}\right\Vert}_2^2 = \sum_{k=-N}^N {\left\vert{p_k}\right\vert}^2 \end{displaymath}$

για κάθε τέτοιο τριγωνομετρικό πολυώνυμο.

4.14 Πέ, 3/4/2014: Το θεώρημα Weierstrass για τριγωνομετρικά πολυώνυμα

Σήμερα χρησιμοποιήσουμε το θεώρημα του Weierstrass για αλγεβρικά πολυώνυμα (ότι δηλ. σε κάθε χώρο τα αλγεβρικά πολυώνυμα είναι πυκνά) για να δείξουμε το αντίστοιχο θεώρημα Weierstrass για τριγωνομετρικά πολυώνυμα: αν $f \in C([0,2\pi])$ ικανοποιεί $f(0) = f(2\pi)$ και $\epsilon>0$ τότε υπάρχει ένα τριγωνομετρικό πολυώνυμο $p(x) = \sum_{n=-N}^N p_n e^{inx}$ (για κάποιο φυσικό αριθμό ) τέτοιο ώστε ${\left\Vert{f-p}\right\Vert}_\infty < \epsilon$ .

4.14.1 Φυλλάδιο ασκήσεων Νο 6

Βρίσκεται εδώ σε μορφή PDF.

4.15 Τρ, 8/4/2014: Ιδιότητες της βέλτιστης ομοιόμορφης πολυωνυμικής προσέγγισης

Ας είναι $f:[a,b]\to{\mathbb{R}}$ μια συνεχής συνάρτηση (ειδικά σε αυτή την παράγραφο κοιτάμε πραγματικές συναρτήσεις και όχι μιγαδικές γιατί μας ενδιαφέρει να μιλήσουμε για μέγιστα και ελάχιστα συναρτήσεων). Επειδή ο χώρος ${\mathcal P}_N$ των πολυωνύμων με βαθμό $\le N$ είναι διάστασης πεπερασμένης ξέρουμε ότι σίγουρα υπάρχει μια βέλτιστη προσέγγιση της από το χώρο ${\mathcal P}_N$ σε οποιαδήποτε νόρμα. Εδώ μας ενδιαφέρουν οι ιδιότητες μιας βέλτιστης προσέγγισης στην ομοιόμορφη νόρμα ( $\infty$ -νόρμα).

Το κύριο θεώρημα που αποδείξαμε είναι το ακόλουθο:

Θεώρημα 1 Έστω $f:[a,b]\to{\mathbb{R}}$ και φυσικός αριθμός. Τότε υπάρχει ακριβώς μια βέλτιστη προσέγγιση $p^*\in{\mathcal P}_N$ της . Ένα πολυώνυμο $p \in {\mathcal P}_N$ είναι το αν και μόνο αν υπάρχει ένα σύνολο τουλάχιστον σημείων του που να είναι εναλασσόμενα για τη συνάρτηση .

4.16 Πέ, 10/4/2014: Τα πολυώνυμα Chebyshev

Σήμερα λύσαμε το εξής πρόβλημα βελτιστοποίησης: αν $n=0,1,2,\ldots$ είναι ένας φυσικός αριθμός ποιο είναι το μονικό πολυώνυμο (δηλ. με μεγιστοβάθμιο συντελεστή ίσο με 1) βαθμού ακριβώς που έχει την ελάχιστη $\infty$ -νόρμα στο διάστημα ;

Αν είναι το τυχόν μονικό πολυώνυμο βαθμού (αυτό σημαίνει ότι $\deg q_n(x) < n$ ) τότε είναι σα να ψάχνουμε ποια είναι η βέλτιστη προσέγγιση του πολυωνύμου από το χώρο πολυωνύμων ${\mathcal P}_{n-1}$ βαθμού στην $\infty$ -νόρμα του .

Χρησιμοποιώντας τις ιδιότητες της βέλτιστης προσέγγισης που αποδείξαμε στο προηγούμενο μάθημα (για τα εναλασσόμενα σημεία που χαρακτηρίζουν τη βέλτιστη προσέγγιση) καταφέραμε να βρούμε το πολυώνυμο

$\begin{displaymath} p_n(x) = 2^{1-n} \cos(n \arccos x). \end{displaymath}$

Από κει ορίσαμε το πολυώνυμο Chebyshev βαθμου

$\begin{displaymath} T_n(x) = \cos(n \arccos x) = 2^{n-1} x^n + \cdots \end{displaymath}$

και αποδείξαμε εύκολα τον αναδρομικό τύπο

$\begin{displaymath} T_n(x) = 2xT_{n-1}(x)-T_{n-2}(x) \end{displaymath}$

μέσω του οποίου υπολογίζεται εύκολα το πολυώνυμο

τουλάχιστον για μικρές τιμές του

4.16.1 Φυλλάδιο ασκήσεων Νο 7

Βρίσκεται εδώ σε μορφή PDF.

4.17 Τρ, 29/4/2014: Παρεμβολή

Ασχοληθήκαμε με το πρόβλημα της παρεμβολής: έχουμε σημεία $x_0, x_1, \ldots, x_N$ ενός χώρου και πραγματικές ή μιγαδικές τιμές $d_0, d_1, \ldots, d_N$ και ψάχνουμε μια συνάρτηση (πάντα με κάποιες προϋποθέσεις γι' αυτή, που συνήθως είναι να ανήκει σε κάποιο γραμμικό χώρο συναρτήσεων) που να παρεμβάλλει τις τιμές στα σημεία , δηλ.

$\begin{displaymath} f(x_j) = d_j, j=0,1,\ldots,N. \end{displaymath}$

Το βασικό θεώρημα που είδαμε είναι ότι αυτό είναι πάντα ένα καλώς τεθιμένο πρόβλημα (έχει δηλ. πάντα μια και μοναδική λύση) όταν τα

είναι πραγματικοί αριθμοί και ο χώρος στον οποίο πρέπει να ανήκει η

είναι ο χώρος ${\mathcal P}_N$ των πολυωνύμων βαθμού $\le N$ .

Είδαμε το πώς λύνεται αυτό το πρόβλημα με τρεις διαφορετικούς τρόπους: την επίλυση γραμμικού συστήματος που καταλήγει σε μια ορίζουσα Vandemonde, την παρεμβολή Lagrange και την παρεμβολή Newton. Κάθε μια από αυτές τις τρεις μεθόδους έχει τα πλεονεκτήματά της και τα συζητήσαμε. Επίσης κάθε μια από αυτές μπορούμε να τη δούμε ως προσδιορισμό του πολυωνύμου παρεμβολής σε μια διαφορετική βάση του χώρου ${\mathcal P}_N$ κάθε φορά. Οι τρεις αυτές βάσεις είναι αντίστοιχα οι

$1, x, x^2, x^3, \ldots, x^N$ ,
$\prod_{k\neq j} (x-x_k)$ , για $j=0, 1, 2, \ldots, N$ ,
$1, (x-x_0), (x-x_0)(x-x_1), \ldots, (x-x_0)(x-x_1)(x-x_2)\cdots(x-x_{N-1})$ .

Είδαμε επίσης το λεγόμενο τύπο του Lagrange με υπόλοιπο (δεν τον αποδείξαμε, δείτε τις σημειώσεις σας όμως).

Τέλος δείξαμε με ένα ενδιαφέρον τοπολογικό επιχείρημα ότι το πρόβλημα της παρεμβολής με συνεχείς συναρτήσεις δεν είναι καλώς τεθιμένο στις δύο ή παραπάνω διαστάσεις, όποιο χώρο συναρτήσεων και να επιλέξουμε για τις παρεμβάλλουσες συναρτήσεις. Ακριβέστερα δείξαμε ότι αν $\Omega \in {\mathbb{R}}^d$ , με $d\ge 2$ , είναι ένα σύνολο με εσωτερικό (περιέχει δηλ. μια ολόκληρη μπάλλα) και αν είναι οποιοσδήποτε ${\mathbb{R}}$ -γραμμικός χώρος συνεχών πραγματικών συναρτήσεων διάστασης τότε πάντα μπορούμε να βρούμε θέσεις

$\begin{displaymath} x_0, x_1, \ldots, x_N \in \Omega \end{displaymath}$

και τιμές

$\begin{displaymath} d_0, d_1, \ldots, d_N \in {\mathbb{R}} \end{displaymath}$

ώστε to πρόβλημα παρεμβολής

$\begin{displaymath} f \in V \mu\epsilon f(x_j) = d_j, j=0, 1, \ldots, N, \end{displaymath}$

να μην έχει λύση.

4.17.1 Φυλλάδιο ασκήσεων Νο 8

Βρίσκεται εδώ σε μορφή PDF.

4.18 Πέ, 1/5/2014: Αργία, δεν έγινε μάθημα

Σήμερα δεν έγινε μάθημα λόγω αργίας.

4.19 Τρ, 6/5/2014: Δεύτερο Διαγώνισμα

Βρίσκεται εδώ σε μορφή PDF.

4.19.1 Βαθμοί 2ου Διαγωνίσματος

Εδώ σε μορφή PDF.

4.20 Πέ, 8/5/2014: Συντελεστές και σειρές Fourier συνεχών, περιοδικών συναρτήσεων

Μιλήσαμε κατ' αρχήν λίγο για την άσκηση 3 του 2ου διαγωνίσματος που μπέρδεψε αρκετό κόσμο.

Έπειτα ορίσαμε τους συντελεστές Fourier συνεχών και $2\pi$ -περιοδικών συναρτήσεων καθώς και τη σειρά Fourier μιας συνάρτησης και τα μερικά αθροίσματα της σειράς. Είδαμε επίσης διάφορες αλγεβρικές ιδιότητες των συντελεστών Fourier (πώς επηρεάζονται αυτοί όταν η συνάρτησή μας υποστεί κάποιες απλές αλλαγές). Λίγο-πολύ κάναμε ό,τι περιέχεται στο Κεφ. 7 των σημειώσεών σας μέχρι και το Πρόβλημα 7.4.

4.20.1 Φυλλάδιο ασκήσεων Νο 9

Βρίσκεται εδώ σε μορφή PDF.

4.21 Τρ, 13/5/2014: Σύγκλιση της σειράς Fourier μιας συνεχούς συνάρτησης στην νόρμα

Σήμερα συνεχίσαμε τη συζήτηση για τους συντελεστές και τη σειρά Fourier μιας συνεχούς και $2\pi$ -περιοδικής συνάρτησης. Είδαμε ότι τα μερικά αθροίσματα της σειράς Fourier της είναι οι βέλτιστες προσεγγίσεις (στην νόρμα) της συνάρτησης από το χώρο των τριγωνομετρικών πολυωνύμων βαθμού $\le N$ , αποδείξαμε την ανισότητα του Bessel και, τέλος, δείξαμε

$\begin{displaymath} {\left\Vert{f - S_Nf}\right\Vert}_2 \to 0 (N\to\infty), \end{displaymath}$

για κάθε συνεχή και $2\pi$ -περιοδική συνάρτηση

. Πόρισμα αυτού του θεωρήματος σύγκλισης είναι και το θεώρημα μοναδικότητας: αν δύο συνεχείς και $2\pi$ -περιοδικές συναρτήσεις έχουν τους ίδιους συντελεστές Fourier τότε πρόκειται για την ίδια συνάρτηση.

4.21.1 ΑΝΑΚΟΙΝΩΣΗ: 3ο διαγώνισμα

Το 3ο και τελευταίο διαγώνισμα θα διεξαχθεί την ώρα του μαθήματος την Πέμπτη 29/5/2014 (τελευταία μέρα του εξαμήνου) και όχι την Τρίτη ως είχε αρχικά ανακοινωθεί.

4.21.2 ΑΝΑΚΟΙΝΩΣΗ: Διαγώνισμα μέσα στην εξεταστική

Όσοι φοιτητές είχαν επιλέξει να εξεταστούν μόνο σε τελικό διαγώνισμα θα πρέπει να επικονωνήσουν μαζί μου για να εξεταστούν προφορικά.

4.22 Πέ, 15/5/2014: Ορθογώνια πολυώνυμα

Είδαμε πρώτα σήμερα τη διαδικασία ορθοκανονικοποίησης Gram-Schmidt, η οποία παίρνει μια, πεπερασμένη ή άπειρη ακολουθία γραμμικώς ανεξαρτήτων διανυσμάτων $f_1, f_2, \cdots$ και παράγει από αυτήν μια ορθοκανονική ακολουθία διανυσμάτων $e_1, e_2, \cdots$ με την ιδιότητα ότι για κάθε $k \ge 1$ έχουμε ${\rm span}{\left\{{f_1, f_2, \ldots, f_k}\right\}} = {\rm span}{\left\{{e_1, e_2, \ldots, e_k}\right\}}$ . Πόρισμα αυτού είναι ότι κάθε χώρος με εσωτερικό γινόμενο πεπερασμένης διάστασης έχει ορθοκανονική βάση.

Έπειτα είδαμε πώς η διαδικασία ορθογωνιοποίησης μπορεί να γίνει ευκολότερα και ταχύτερα όταν πρόκειται για ένα γραμμικό χώρο πολυωνύμων με εσωτερικό γινόμενο του τύπου ${\langle f, g \rangle} = \int_a^b f(x) \overline{g(x)} w(x) dx$ , όπου είναι μια συνάρτηση βάρους. Στην περίπτωση αυτή είδαμε μια πολύ γρήγορη διαδικασία με την οποία παράγεται μια ακολουθία

$\begin{displaymath} Q_0(x), Q_1(x), Q_2(x), \cdots \end{displaymath}$

από μονικά πολυώνυμα βαθμού $\deg{Q_i} = i$ , τα οποία είναι ορθογώνια μεταξύ τους ως προς το άνω εσωτερικό γινόμενο. Αποδείξαμε μάλιστα ότι μια τέτοια ακολουθία πολυωνύμων είναι μοναδική.

4.22.1 Φυλλάδιο ασκήσεων Νο 10

Βρίσκεται εδώ σε μορφή PDF.

4.23 Τρ, 20/5/2014: Ρίζες ορθογωνίων πολυωνύμων. Μέθοδοι αριθμητικής ολοκλήρωσης.

Αποδείξαμε πρώτα σήμερα το θεώρημα 8.3 των σημειώσεων, που λέει ότι για μια συνεχή και θετική συνάρτηση βάρους σε ένα φραγμένο διάστημα η ακολουθία των ορθογωνίων πολυωνύμων έχει όλες τις ρίζες απλές και στο εσωτερικό του διαστήματος. Αυτό θα μας φανεί χρήσιμο αργότερα στις μεθόδους αριθμητικής ολοκλήρωσης.

Έπειτα κάναμε μια εισαγωγή στις απλές μεθόδους αριθμητικής ολοκλήρωσης, δώσαμε μερικά παραδείγματα, ορίσαμε την τάξη ενός απλού κανόνα αριθμητικής ολοκλήρωσης και διατυπώσαμε τη σχέση που έχει η τάξη μιας μεθόδους με την ακρίβειά της (Θεώρημα 9.1 των σημειώσεων).

4.24 Πέ, 22/5/2014: Κανόνες ολοκλήρωσης Gauss

Αποδείξαμε σήμερα ότι αν ένας απλός κανόνας ολοκλήρωση έχει τάξη (ολοκληρώνει δηλ. ακριβώς όλα τα πολυώνυμα βαθμού $\le r$ ) τότε αν γράψουμε για τον αντίστοιχο σύνθετο κανόνα ολοκλήρωσης στο διάστημα χωρισμένο σε ίσα διαστήματα

$\begin{displaymath} I_N(f) = \sum_{j=0}^{N-1} I_*(f, [x_j, x_{j+1}]), \left(x_j = A+j\frac{B-A}{N}\right), \end{displaymath}$

τότε το σφάλμα ολοκλήρωσης

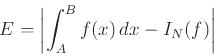
$\begin{displaymath} E = {\left\vert{\int_A^Bf(x) dx - I_N(f)}\right\vert} \end{displaymath}$

ικανοποιεί την ανισότητα

$\begin{displaymath} E \le \frac{C}{N^{r+1}}, \end{displaymath}$

όπου

είναι μια θετική ποσότητα που εξαρτάται από το διάστημα και τη συνάρτηση αλλά δεν εξαρτάται από το

(Θεώρημα 9.1 των σημειώσεων). Το νόημα αυτού του αποτελέσματος είναι ότι μας δίνει την εξάρτηση του (άνω φράγματος του) σφάλματος από το

, αν κρατήσουμε το πρόβλημα σταθερό (δεν αλλάξουμε δηλ. το διάστημα και τη συνάρτηση αλλά μόνο την παράμετρο

που δεν είναι μέρος του προβλήματος και είναι στη διάθεσή μας να την αλλάξουμε προκειμένου να πετύχουμε καλύτερη εγγύηση για το σφάλμα της ολοκλήρωσης).

Είδαμε έπειτα ότι αν κάποιος μας έχει προδιαγράψει τα σημεία $x_j \in [a, b]$ σε ένα απλό κανόνα ολοκλήρωσης στο

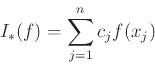
$\begin{displaymath} I_*(f) = \sum_{j=1}^n c_j f(x_j) \end{displaymath}$

τότε πάντα μπορούμε να επιλέξουμε τους συντελεστές

έτσι ώστε ο κανόνας

να έχει τάξη $\ge n-1$ .

Τέλος είδαμε ότι αν μας επιτραπεί, πέρα από τους συντελεστές , να επιλέξουμε και τα σημεία $x_1, x_2, \ldots, x_n \in (a,b)$ τότε αν επιλέξουμε αυτά να είναι οι ρίζες του πολυωνύμου (όπου $Q_0(x), Q_1(x), \cdots$ είναι η ακολουθία μονικών ορθογωνίων πολυωνύμων για το διάστημα με συνάρτηση βάρους $w(x) \equiv 1$ , και γνωρίζουμε από το Θεώρημα 8.3 των σημειώσεων ότι το έχει απλές ρίζες στο ) τότε μπορούμε να επιλέξουμε τους συντελεστές (όπως και στην προηγούμενη παράγραφο) ώστε ο κανόνας ολοκλήρωσης να έχει τάξη $\ge 2n-1$ . Αυτοί οι κανόνες ολοκλήρωσης ονομάζονται κανόνες ολοκλήρωσης Gauss.