![$p:\Omega\to[0,1]$](img3.png){kind=small}
που μας λέει ποια είναι η πιθανότητα
εμφάνισης του κάθε αποτελέσματος. Είδαμε πώς αυτή η συνάρτηση επεκτείνεται σε μια συνολοσυνάρτηση
πάνω στα υποσύνολα του 
(ενδεχόμενα) τουλάχιστον όταν ο δειγματικός χώρος είναι πεπερασμένος
ή αριθμήσιμος.
``I think you're begging the question,'' said Haydock, ``and I can see looming ahead one of those terrible exercises in probability where six men have white hats and six men have black hats and you have to work it out by mathematics how likely it is that the hats will get mixed up and in what proportion. If you start thinking about things like that, you would go round the bend. Let me assure you of that!''
Agatha Christie, The mirror crack'd from side to side (1962).
Τρίτη 5-7, Πέμπτη 4-5 στο Αμφ. ΣΠ. Έναρξη μαθημάτων: 3/10/06.
Ώρες γραφείου: Τε 11-1 (Γ 111, προκατ κτήριο στην Κνωσό)
Δίωρο ασκήσεων: Τετάρτη 1-3, Θ 201 και Θ 207. Τα ονόματα των βοηθών θα ανακοινωθούν.
Από τον οδηγό σπουδών του Τμ. Μαθηματικών:
Επίσης, έχουν μπεί κάποια κλασικά βιβλία πιθανοτήτων στην κλειστή συλλογή της βιβλιοθήκης.
Οι διδακτικές σημειώσεις βρίσκονται εδώ σε μορφή PDF. Προσέξτε την ημερομηνία του αρχείου για να δείτε πότε ενημερώθηκαν οι σημειώσεις για τελευταία φορά.
Λόγω του ότι οι σημειώσεις αυτές γράφονται κατά τη διάρκεια του μαθήματος οι συχνές αλλαγές σε αυτές θα είναι αναπόφευκτες, αν και, ελπίζω, όχι σημαντικές. Ιδιαίτερα οι αριθμοί προβλημάτων, παραδειγμάτων κλπ αναμένεται ότι θα αλλάζουν συχνά, πράγμα που μπορεί να δημιουργήσει μερικά προβλήματα συνεννόησης.
Περίοδος Ιανουαρίου: Θα δοθούν τρία (3) υποχρεωτικά διαγωνίσματα κατά τη διάρκεια του εξαμήνου (ένα από αυτά, κατά την εξεταστική περίοδο). Κάθε ένα από αυτά θα μετράει για το 1/3 του συνολικού βαθμού. Το διαγώνισμα θα δοθεί στις 2/11/06, 4-5, και το δεύτερο στις 7/12/06, 4-5.
Περίοδος Σεπτεμβρίου: Ο βαθμός γι' αυτή την περίοδο θα εξαρτάται μόνο από την εξέταση του Σεπτεμβρίου.
Η σελίδα αυτή θα ενημερώνεται τουλάχιστον μετά από κάθε μάθημα και σκοπό έχει να μεταδίδει μερικές βασικές χρήσιμες πληροφορίες για το περιεχόμενο του μαθήματος (π.χ. τι να προσέξετε, υποδείξεις για λύσεις των ασκήσεων, κ.ά.) καθώς και για διαδικαστικά θέματα.
Σπανίως θα βγαίνουν ανακοινώσεις που αφορούν το μάθημα σε χαρτί. Παρακαλώ να συμβουλεύεστε αυτηή τη σελίδα τουλάχιστον 2-3 φορές την εβδομάδα.
Είδαμε διάφορα παραδείγματα όπου η διαίσθησή μας όσον αφορά το τι σημαίνει πιθανότητα είναι σωστή και εύκολη όπως και κάποια παραδείγματα όπου είναι σαφές ότι χρειάζεται περισσότερο ποσοτική μελέτη.
Ορίσαμε το δειγματικό χώρο ως χώρο όλων των δυνατών αποτελεσμάτων ενός πειράματος
συνοδευόμενο από μια συνάρτηση
που μας λέει ποια είναι η πιθανότητα
εμφάνισης του κάθε αποτελέσματος. Είδαμε πώς αυτή η συνάρτηση επεκτείνεται σε μια συνολοσυνάρτηση
πάνω στα υποσύνολα του (ενδεχόμενα) τουλάχιστον όταν ο δειγματικός χώρος είναι πεπερασμένος
ή αριθμήσιμος.
Δείξαμε διάφορες βασικές ιδιότητες της συνολοσυνάρτησης της πιθανότητας.
Αύριο Πέ, 5/10/06, δε θα γίνει το μάθημα λόγω προγραμματισμένης διακοπής ρεύματος:
From: Tsalimi Katerina Sent: Wednesday, October 04, 2006 11:30 AM Subject: diakopi revmatos avrio Avrio Pempti 8a ginei diakopi revmatos apo ti DEH 3.30-5.30 kai den 8a yparxei fws sta prokat. Milisa me tin ka Papadopoulou i opoia mou eipe oti den mporei na ginei ma8ima autes tis wres sta amfi8eatra, logw mi eparkous fwtismou. Autes tis wres ta amfi8eatra einai kleismena apo to Tmima Epistimis Ypologistwn kai apo to Ma8imatiko. Parakalw enimerwste tous didaskontes sas gia anaboli twn ma8imatwn. Katerina Tsalimi Grammateia Kosmiteias Sxolis 8etikwn kai Texnologikwn Epistimwn Panepistimio Kritis T.8. 2208, L. Knwsou 71409 Irakleio Kritis til. 2810 393200 fax: 2810 393202
Το πρώτο διαγώνισμα θα γίνει την Πέμπτη 2/11/06, την ώρα του μαθήματος, και το δεύτερο την Πέμπτη 7/12/06, επίσης τν ώρα του μαθήματος.
Οι σημειώσεις του μαθήματος έχουν αρχίσει να εμφανίζονται. Δείτε §2.1.
Ορίσαμε την έννοια της υπό συνθήκην πιθανότητας ενός ενδεχομένου 
ως προς ένα ενδεχόμενο 
,
εφ' όσον
![${{\bf {Pr}}\left[{B}\right]}>0$](img7.png){kind=small}
, να είναι η ποσότητα
![${{\bf {Pr}}\left[{A \vert B}\right]} = {{\bf {Pr}}\left[{A { \vert }B}\right]} / {{\bf {Pr}}\left[{B}\right]}$](img8.png){kind=small}
.
Είδαμε επίσης διάφορα παραδείγματα εφαρμογής της.
Μιλήσαμε για την ανεξαρτησία ενδεχομένων. Είδαμε ότι τις περισσότερες φορές αυτή μας δίδεται αξιωματικά στην περιγραφή του πειράματος. Αναλύσαμε με κάποια λεπτομέρεια μερικά ενδεχόμενα όταν το πείραμα αφορά 4 ρίψεις ενός τιμίου νομίσματος.
Οι σημειώσεις έχουν ενημερωθεί με το υλικό που έχουμε ήδη καλύψει και παραπάνω.
Οι σημειώσεις έχουν ενημερωθεί με το υλικό που έχουμε ήδη καλύψει και παραπάνω.
Είδαμε διάφορα προβλήματα στα οποία πρέπει να εκμεταλλευτούμε την ανεξαρτησία ενδεχομένων για να βρούμε την απάντηση. Επίσης αρχίσαμε να ασχολούμαστε με το κεφάλαιο που αφορά το μέτρημα, και είδαμε τη βασική αρχή του μετρήματος που είναι ότι μπορούμε να πολλαπλασιάζουμε το πλήθος των δυνατών επιλογών που κάνουμε, φτάνει οι μέχρι κάποια στιγμή επιλογές μας να μην επηρεάζουν το πλήθος των μετέπειτα επιλογών μας (ημιανεξαρτησία).
Έχω αφήσει στο κυλικείο για φωτοτύπηση τις σημειώσεις που έχω γράψει μέχρι σήμερα.
Δυστυχώς το μάθημα σήμερα περιορίστηκε σε 15 λεπτά αφού διακόπηκε από φοιτητές είχαν προγραμματίσει γενική συνέλευση στο διπλανό αμφιθέατρο. Σε αυτά τα 15 λεπτά έγιναν διάφορα παραδείγματα απαρίθμησης.
Το πρώτο διαγώνισμα του μαθήματος (Πέ, 2/11/06, ώρα του μαθήματος) θα είναι παρόμοιο με αυτό (PDF).
Λόγω της κατάληψης που πραγματοποιούν οι φοιτητές του Τμήματος Μαθηματικών το πρώτο διαγώνισμα μετατίθεται για το Σάββατο 4/11/06, 10-11 το πρωί, στα Αμφιθέατρα ΒΞ και ΣΠ.
Επίσης, την Παρασκευή 3/11/06, και ώρα 20:00-22:00 θα γίνει μάθημα στο Αμφ ΒΞ. Το αντικείμενο θα είναι η λύση παραδειγμάτων και προβλημάτων (μπορείτε να το δείτε και ως προετοιμασία για το διαγώνισμα).
Κάναμε διάφορα παραδείγματα απαρίθμησης και λύσαμε το υπόδειγμα του 1ου διαγωνίσματος.
Είχαμε το πρώτο μας διαγώνισμα, 10-11 το πρωί. Τα αποτελέσματα μπορείτε να τα δείτε εδώ ταξινομημένα κατά ΑΜ και εδώ ταξινομημένα κατά βαθμό.
αντικειμένων ανά 
. Διωνυμικό θεώρημα.
Είδαμε πώς να υπολογίζουμε το πλήθος των υποσυνόλων μεγέθους ενός συνόλου με
αντικείμενα. Εφαρμόσαμε αυτόν τον υπολογισμό σε διάφορα προβλήματα επιλογής.
Είδαμε διάφορες ταυτότητες που πληρούνται από το διωνυμικό συντελεστή 
,
. Τέλος είδαμε το διωνυμικό θεώρημα
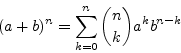
Είδαμε την έννοια της τυχαίας μεταβλητής (ΤΜ) και την έννοια της πυκνότητας
πιθανότητας μιας διακριτής ΤΜ (μιας ΤΜ δηλ. που παίρνει ένα σύνολο τιμών 
που είναι
αριθμήσιμο σύνολο). Υπολογίσαμε σε διάφορα απλά παραδείγματα τη συνάρτηση πυκνότητας πιθανότητας.
Την Τρίτη 14/11/06 δε θα γίνει το μάθημα λόγω αναστολής της λειτουργίας του Πανεπιστημίου Κρήτης.
ΠΡΑΚΤΙΚΑ 235ης/26-10-2006 ΣΥΝΕΔΡΙΑΣ ΤΗΣ ΣΥΓΚΛΗΤΟΥ ΤΟΥ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ Θέματα Ακαδημαϊκά Θέμα: 1ο Kαταλογισμοί σε μέλη ΔΕΠ. Εικοσιτετράωρη αναστολή λειτουργίας του Πανεπιστημίου Κρήτης. Τα μέλη της Συγκλήτου, αφού ενημερώθηκαν από τον κ. Πρύτανη και την κ. Μ. Κεντούρη για την εκδίκαση της υπόθεσης που αφορά τους καταλογισμούς σε μέλη ΔΕΠ στις 14-11-2006, ενώπιον του Ελεγκτικού Συνεδρίου κατέληξαν: «ΕΙΚΟΣΙΤΕΤΡΑΩΡΗ ΑΝΑΣΤΟΛΗ ΛΕΙΤΟΥΡΓΙΑΣ ΤΟΥ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ Όπως είναι γνωστό, στα μέλη της Επιτροπής Ερευνών του Πανεπιστημίου Κρήτης κατά την περίοδο 2002-2004 έχουν καταλογισθεί δαπάνες του Ειδικού Λογαριασμού Κονδυλίων Έρευνας, των οποίων, χωρίς να αμφισβητείται η νομιμότητα, δεν αναγνωρίσθηκε η σκοπιμότητα από τον έλεγχο των Οικονομικών Επιθεωρητών. Οι δαπάνες αυτές αφορούν σε μισθούς συμβασιούχων υπαλλήλων, οι οποίοι έχουν εν τω μεταξύ μονιμοποιηθεί διότι κάλυπταν πάγιες και διαρκείς ανάγκες του Πανεπιστημίου, καθώς και δαπάνη για τη συμπληρωματική ασφάλιση όλου του προσωπικού που έγινε για να αντιμετωπισθούν σοβαρές ελλείψεις στην κάλυψη που προσφέρει το Ελληνικό Δημόσιο στους εργαζομένους στο Πανεπιστήμιο. Το Πανεπιστήμιο Κρήτης εξ αρχής θεώρησε ότι οι εν λόγω δαπάνες έγιναν μέσα από νόμιμες διαδικασίες για το συμφέρον του Ιδρύματος, εντός των σκοπών του Ε.Λ.Κ.Ε. και χωρίς να δημιουργηθεί οποιοδήποτε έλλειμμα. Οι σχετικές αποφάσεις, που ελήφθησαν από την Επιτροπή Ερευνών με τη συμμετοχή των συναδέλφων, ως εκπροσώπων των Τμημάτων τους, σε κάθε περίπτωση είτε είχαν τη σύμφωνη γνώμη της Συγκλήτου, είτε ακολουθούσαν αποφάσεις της. Η ακαδημαϊκή κοινότητα του Πανεπιστημίου Κρήτης εξακολουθεί να στέκεται αλληλέγγυα στους συναδέλφους που διώκονται, και να θεωρεί ότι στο πρόσωπό τους διώκεται το Πανεπιστήμιο Κρήτης. Η Σύγκλητος του Πανεπιστημίου Κρήτης αποφάσισε ομόφωνα να αναστείλει την λειτουργία του Ιδρύματος την 14η Νοεμβρίου 2006, ημέρα κατά την οποία εκδικάζεται ενώπιον του Ελεγκτικού Συνεδρίου η αίτηση των συναδέλφων αναστολής της εκτέλεσης της καταλογιστικής πράξης μέχρι η υπόθεση να εκδικαστεί επί της ουσίας. Το μέτρο αυτό συνιστά ελάχιστη εκδήλωση συμπαράστασης προς τους συναδέλφους οι οποίοι ανιδιοτελώς και σύννομα ενήργησαν στο πλαίσιο συλλογικών οργάνων για τους σκοπούς που έχει ταχθεί να υπηρετεί το Πανεπιστήμιο Κρήτης.» Ακριβές απόσπασμα Ρέθυμνο, 6-11-2006 Η Γραμματέας της Συγκλήτου Μαρία Νεονάκη
(Το μάθημα θα αναπληρωθεί μέσα στην ίδια εβδομάδα σε ώρα που θα ανακοινωθεί.)
Την Πέμπτη 16/11, ώρα 7-9 το βράδυ θα γίνει δίωρο μάθημα στο Αμφ. Α (η αίθουσα δεν έχει κλειστεί ακόμη οπότε υπάρχει μια μικρή πιθανότητα αλλαγής).
Για μια διακριτή ΤΜ 
ορίσαμε τη συνάρτηση πυκνότητάς της
![$f_X(n) = {{\bf {Pr}}\left[{X = n}\right]}$](img14.png){kind=small}
και τη συνάρτηση κατανομής της
![$F_X(n) = {{\bf {Pr}}\left[{X \le n}\right]}$](img15.png){kind=small}
. Επίσης ορίσαμε την έννοια
της ανεξαρτησίας μιας οικογένειας ΤΜ και είδαμε πώς βρίσκουμε την πυκνότητα της
αν οι 
είναι ανεξάρτητες και γνωρίζουμε τις πυκνότητές τους.
Ορίσαμε τη μέση τιμή μιας ΤΜ που παίρνει ακέραιες τιμές και υπολογίσαμε διάφορα παραδείγματα.
Έχουν ενημερωθεί οι σημειώσεις και έχει δοθεί το Κεφ. 4 στο κυλικείο για φωτοτύπηση.
Είδαμε πώς ορίζεται η μέση τιμή μιας ΤΜ που είναι διακριτή αλλά όχι κατ' ανάγκη με
ακέραιες τιμές. Επίσης είδαμε την ιδιότητα της γραμμικότητας, η οποία είναι πάρα πολύ χρήσιμη,
είδαμε πώς υπολογίζουμε τη μέση τιμή της 
χωρίς να υπολογίσουμε πρώτα την πυκνότητα
της , και τέλος είδαμε ότι αν οι και 
είναι ανεξάρτητες τότε
![${{\bf E}\left[{XY}\right]} = {{\bf E}\left[{X}\right]}\cdot{{\bf E}\left[{Y}\right]}$](img20.png){kind=small}
. Λύσαμε διάφορα προβλήματα.
Λύσαμε διάφορα προβλήματα (μέσα από τις σημειώσεις). Χρησιμοποιήσαμε πολλές φορές το «σπάσιμο» μιας ΤΜ σαν άθροισμα άλλων απλούστερων, που είναι συχνά ΤΜ που παίρνουν μόνο τις τιμές 0 ή 1. Αυτό συχνά διευκολύνει υπολογισμούς ΤΜ, λόγω της γραμμικότητας της μέσης τιμής. Επίσης ορίσαμε τη διασπορά μιας ΤΜ που έχει μέση τιμή και είδαμε μερικές απλές ιδιότητες αυτής.
Είδαμε ότι η διασπορά του αθροίσματος ΤΜ που είναι ανεξάρτητες ανά δύο ισούται με το άθροισμα των διασπορών. Επίσης είδαμε αρκετά παραδείγματα υπολογισμού διασποράς. Επίσης είδαμε τις ανισότητες του Markov και του Chebyshev και τις συγκρίναμε σε ένα απλό παράδειγμα.
Ορίσαμε την έννοια της γεννήτριας συνάρτησης
![$\Phi(t) = {{\bf E}\left[{t^X}\right]}$](img21.png){kind=small}
μιας ΤΜ
.
Είδαμε παραδείγματα υπολογισμού (διωνυμική, Poisson) και ότι η γεννήτρια του αθροίσματος ανεξαρτήτων είναι το γινόμενο των γεννητριών. Επίσης είδαμε χωρίς απόδειξη ότι δύο ΤΜ με ίδια γεννήτρια συνάρτηση είναι ισόνομες.
Χρησιμοποιήσαμε γεννήτριες συναρτήσεις για να δείξουμε ότι το άθροισμα ανεξαρτήτων
διωνυμικών με ίδιο 
είναι επίσης διωνυμική (το δείξαμε αυτό και χωρίς γεννήτριες
συναρτήσεις) και επίσης ότι το άθροισμα ανεξαρτήτων Poisson είναι επίσης Poisson.
Οι σημειώσεις του μαθήματος έχουν συμπληρωθεί και με το σημερινό μάθημα περί γεννητριών συναρτήσεων (§4.4).
Στο διαγώνισμα της επόμενης Πέμπτης 7/12/06 να έχετε διαβάσει όλα όσα έχουμε κάνει μέχρι και σήμερα (μέχρι δηλ. την §4.4). Το διαγώνισμα θα είναι παρόμοιας μορφής με το πρώτο αλλά η έμφαση θα είναι στις έννοιες που κάναμε μετά το πρώτο διαγώνισμα. Θα υπάρχουν όμως και 1-2 ασκήσεις που θα αφορούν έννοιες στις οποίες εξεταστήκατε ήδη στο πρώτο διαγώνισμα.
Είδαμε την έννοια της κοινής πυκνότητας 
ενός ζεύγους ΤΜ καθώς και το πώς
προκύπτουν οι λεγόμενες περιθώριες πυκνότητες 
και 
από αυτή. Είδαμε διάφορα παραδείγματα.
Έγινε σήμερα στην ώρα του μαθήματος το δεύτερο διαγώνισμα. Μπορείτε να δείτε τους βαθμούς εδώ κατά ΑΜ και εδώ κατά βαθμό.
Λύσαμε τις ασκήσεις του διαγωνίσματος:
παίρνει τις τιμές 1 και 3/2 με ίση πιθανότητα και την τιμή 2
με διπλάσια πιθανότητα από την 1. Βρείτε τη
![${{\bf E}\left[{X}\right]}$](img28.png){kind=small}
.
είναι
πυκνότητα πιθανότητας στους ακεραίους. Βρείτε το 
.
είναι
πυκνότητα πιθανότητας. Βρείτε το .
και είναι ανεξάρτητες και
![${{\bf E}\left[{X^4}\right]} = 2, {{\bf E}\left[{X^2}\right]} = {{\bf E}\left[{Y^2}\right]} = 1,
{{\bf E}\left[{Y}\right]} = 0$](img32.png){kind=small}
τότε βρείτε τη
![${{\bf Var}\left[{X^2Y}\right]}$](img33.png){kind=small}
.
φορές και έστω το πλήθος των φορών
που φέρνουμε 1 ή 2. Βρείτε τη
.
φορές ένα νόμισμα που φέρνει κορώνα με πιθανότητα και έστω το πλήθος των διατεταγμένων ζευγών
, με 
, τέτοια ώστε το αποτέλεσμα της 
και της 
ρίψης είναι το ίδιο.
Βρείτε τη
.
με ένα από τρία χρώματα. Κάθε
χρώμα χρησιμοποιείται με την ίδια πιθανότητα σε κάθε στοιχείο. Έστω το πλήθος των
τριμελών υποσυνόλων του που τα στοιχεία τους έχουν όλα το ίδιο χρώμα.
Βρείτε τη
.
ρίψη
τότε κερδίζουμε 
(
).
Πόσο είναι το μέσο κέρδος μας?
ρίψη
τότε κερδίζουμε 
().
Πόσο είναι το μέσο κέρδος μας?
το πόσες μαύρες περισσότερες από άσπρες έχουμε (το είναι προσημασμένη ποσότητα).
Βρείτε τη
.
Λύσαμε ασκήσεις.
Λύσαμε ασκήσεις.
Δεν έγινε μάθημα λόγω του ότι δεν ήρθε κανείς φοιτητής.
Μετά τις διακοπές των Χριστουγέννων δε θα γίνουν άλλες διαλέξεις δικές μου. Θα γίνονται όμως κανονικά οι ασκήσεις της Τετάρτης, και συνιστώ έντονα να τις παρακολουθήσετε για προετοιμαστείτε για την τελική εξέταση.
Το τελικό διαγώνισμα θα γίνει στις 16/7/07, στις 13:00. Η μορφή του θα είναι παρόμοια με τα δύο προηγούμενα διαγωνίσματα η εξεταστέα ύλη είναι ακριβώς η ύλη που διδάχτηκε σε ολόκληρο το εξάμηνο.
Βρίσκονται εδώ.