



Next: 5.2 Πα, 27/9/02: Μικρή
Up: 5 Ημερολόγιο Μαθήματος (Διδακτικές
Previous: 5 Ημερολόγιο Μαθήματος (Διδακτικές
Contents
Μιλήσαμε κατ' αρχήν για ορισμένες έννοιες τις οποίες θα μελετήσουμε κατά τη διάρκεια
του εξαμήνου. Το μάθημα συνίσταται ουσιαστικά σε μια μελέτη ορισμένων μοντέλων
υπολογισμού, ή, αντίστοιχα, στη μελέτη κλάσσεων γλωσσών που αναγνωρίζονται από τα
μοντέλα αυτά. Το μοντέλο υπολογισμού από το οποίο θα αρχίσουμε είναι η λεγόμενη
μηχανή πεπερασμένων καταστάσεων και η αντίστοιχη κλάσση γλωσσών που αναγνωρίζονται
από μηχανές πεπερασμένων καταστάσεων είναι οι κανονικές γλώσσες
(regular languages).
Ορίσαμε τις έννοιες:
- Αλφάβητο
 είναι ένα οποιδήποτε πεπερασμένο σύνολο, του οποίου
τα στοιχείά ονομάζουμε σύμβολα ή γράμματα.
Π.χ.
είναι ένα οποιδήποτε πεπερασμένο σύνολο, του οποίου
τα στοιχείά ονομάζουμε σύμβολα ή γράμματα.
Π.χ.
 ή
ή  = όλα τα γράμματα και
σημεία στίξης της Ελληνικής γλώσσας.
= όλα τα γράμματα και
σημεία στίξης της Ελληνικής γλώσσας.
- Λέξη πάνω από ένα αλφάβητο
 λέγεται μια πεπερασμένη ακολουθία
γραμμάτων του
λέγεται μια πεπερασμένη ακολουθία
γραμμάτων του  , ενδεχομένως και κενή (η κενή λέξη συμβολίζεται
πάντα με το
, ενδεχομένως και κενή (η κενή λέξη συμβολίζεται
πάντα με το 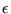 ). Π.χ. αν
). Π.χ. αν
 τότε
τότε
 είναι μια λέξη πάνω από το
είναι μια λέξη πάνω από το  , με μήκος
, με μήκος
 .
Η κενή λέξη
.
Η κενή λέξη 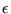 έχει μήκος 0.
έχει μήκος 0.
- Μια γλώσσα
 πάνω από ένα αλφάβητο
πάνω από ένα αλφάβητο  είναι ένα
οποιοδήποτε σύνολο, πεπερασμένο ή άπειρο, λέξεων πάνω από το
είναι ένα
οποιοδήποτε σύνολο, πεπερασμένο ή άπειρο, λέξεων πάνω από το  .
Π.χ., αν
.
Π.χ., αν
 το σύνολο
είναι η γλώσσα όλων των δυαδικών λέξεων με μήκος που είναι τέλειο
τετράγωνο.
Μια γλώσσα
το σύνολο
είναι η γλώσσα όλων των δυαδικών λέξεων με μήκος που είναι τέλειο
τετράγωνο.
Μια γλώσσα  μπορεί να περιέχει την κενή λέξη ή όχι.
μπορεί να περιέχει την κενή λέξη ή όχι.
- Αν
 και
και
 είναι δύο λέξεις πάνω από το
είναι δύο λέξεις πάνω από το  με μήκη
με μήκη  και
και  , τότε ορίζουμε τη συγκόλληση (concatenation)
, τότε ορίζουμε τη συγκόλληση (concatenation)
 να είναι η λέξη
να είναι η λέξη
 , που έχει μήκος
το άθροισμα των μηκών.
Προφανώς ισχύει πάντα
, που έχει μήκος
το άθροισμα των μηκών.
Προφανώς ισχύει πάντα
 ,
για κάθε λέξη
,
για κάθε λέξη 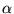 .
.
Μια λέξη  λέγεται πρόθεμα (prefix) μιας λέξης
λέγεται πρόθεμα (prefix) μιας λέξης 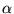 αν υπάρχει λέξη
αν υπάρχει λέξη
 τ.ώ.
τ.ώ.
 . Ομοίως η
. Ομοίως η  λέγεται επίθεμα (suffix)
της
λέγεται επίθεμα (suffix)
της 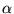 αν υπάρχει
αν υπάρχει  τ.ώ.
τ.ώ.
 .
Είναι φανερό ότι μια λέξη με μήκος
.
Είναι φανερό ότι μια λέξη με μήκος  έχει ακριβώς
έχει ακριβώς  προθέματα και άλλα
τόσα επιθέματα.
προθέματα και άλλα
τόσα επιθέματα.
- Αν
 είναι δύο γλώσσες πάνω από το
είναι δύο γλώσσες πάνω από το  ορίζουμε τη γλώσσα
Ορίζουμε επίσης
ορίζουμε τη γλώσσα
Ορίζουμε επίσης
 και για
και για 
 (συγκόλληση της
(συγκόλληση της  με τον εαυτό της
με τον εαυτό της
 φορές).
Τέλος ορίζουμε
και
Με βάση αυτούς τους συμβολισμούς, και παρατηρώντας ότι με
φορές).
Τέλος ορίζουμε
και
Με βάση αυτούς τους συμβολισμούς, και παρατηρώντας ότι με  πέρα
από το αλφάβητο συμβολίζουμε και τη γλώσσα πάνω από το
πέρα
από το αλφάβητο συμβολίζουμε και τη γλώσσα πάνω από το  με στοιχεία
όλες τις λέξεις πάνω από το
με στοιχεία
όλες τις λέξεις πάνω από το  με ένα ακριβώς γράμμα, έχουμε ότι
με ένα ακριβώς γράμμα, έχουμε ότι
 είναι η γλώσσα όλων των λέξεων πάνω από το
είναι η γλώσσα όλων των λέξεων πάνω από το  και
και  είναι η γλώσσα όλων των μη κενών λέξεων πάνω από το
είναι η γλώσσα όλων των μη κενών λέξεων πάνω από το  .
Έτσι, αντί να λέμε ότι
.
Έτσι, αντί να λέμε ότι  είναι μια γλώσσα πάνω από το
είναι μια γλώσσα πάνω από το  γράφουμε
απλώς
γράφουμε
απλώς
 .
.
Για να βεβαιωθείτε ότι έχετε καταλάβει το περιεχόμενο της σημερινής διάλεξης
βεβαιωθείτε ότι καταλαβαίνετε τι περιγράφει η γλώσσα
Αυτή είναι η συγκόλληση τριών γλωσσών, της
 ,
της
,
της  (συντομογραφία της γλώσσας
(συντομογραφία της γλώσσας
 με ένα στοιχείο) και
της
με ένα στοιχείο) και
της
 .
Όταν, όπως εδώ, δεν περιγράφουμε το αλφάβητο, αυτό συνάγεται από όλα
τα σύμβολα που έχουν χρησιμοποιηθεί, στην προκειμένη περίπτωση
δηλαδή
.
Όταν, όπως εδώ, δεν περιγράφουμε το αλφάβητο, αυτό συνάγεται από όλα
τα σύμβολα που έχουν χρησιμοποιηθεί, στην προκειμένη περίπτωση
δηλαδή
 .
.
- Ένα κατευθυνόμενο γράφημα είναι μια συλλογή από κορυφές και
ακμές που τις ενώνουν, όπως στο σχήμα παρακάτω.
Λέγεται κατευθυνόμενο επειδή υπάρχει η έννοια της κατεύθυνσης
πάνω στις ακμές. Οι δε ακμές μπορούν να ενώνουν και μια κορυφή
με τον εαυτό της, όπως επίσης μπορούν να υπάρχουν και πολλαπλές ακμές
που ενώνουν το ίδιο ζεύγος κορυφών.
Σχήμα 1. Ενα κατευθυνόμενο γράφημα με 4 κορυφές και 6 ακμές.
Σε ένα γράφημα δεν έχει καμία σημασία ο τρόπος που το σχεδιάζουμε πάνω
στο χαρτί, αλλά αυτό που μας ενδιαφέρει είναι μόνο ποια κορυφή συνδέεται
με ποια.
Σε ένα τέτοιο γράφημα μονοπάτι αποτελεί μια οποιαδήποτε πεπερασμένη
ακολουθία διαδοχικών κορυφών. Οι κορυφές  και
και  λέγονται
διαδοζικές αν υπάρχει η ακμή
λέγονται
διαδοζικές αν υπάρχει η ακμή  .
Έτσι, στο σχήμα που φαίνεται παραπάνω το 24231 είναι ένα μονοπάτι
μήκους 4 (το μήκος είναι το πόσες ακμές διανύονται στο μονοπάτι).
Αν αρχή και τέλος του μονοπατιού συμπίπτουν αυτό λέγεται κύκλος,
π.χ. το 424.
.
Έτσι, στο σχήμα που φαίνεται παραπάνω το 24231 είναι ένα μονοπάτι
μήκους 4 (το μήκος είναι το πόσες ακμές διανύονται στο μονοπάτι).
Αν αρχή και τέλος του μονοπατιού συμπίπτουν αυτό λέγεται κύκλος,
π.χ. το 424.
Άσκηση 5.1.1
Πόσες λέξεις μήκους

υπάρχουν πάνω από ένα αλφάβητο με

γράμματα;
Άσκηση 5.1.2
Δείξτε ότι για κάθε γλώσσα

και φυσικούς αριθμούς

ισχύει

.
Άσκηση 5.1.3
Έστω κατευθυνόμενο γράφημα

με

κορυφές και μονοπάτι στο

μέ
μήκος

.
Δείξτε ότι το μονοπάτι περιέχει ένα κύκλο,
ένα υπομονοπάτι δηλ. του τύπου

με

.
Mihalis Kolountzakis
2003-09-04
![]() λέγεται πρόθεμα (prefix) μιας λέξης
λέγεται πρόθεμα (prefix) μιας λέξης ![]() αν υπάρχει λέξη
αν υπάρχει λέξη
![]() τ.ώ.
τ.ώ.
![]() . Ομοίως η
. Ομοίως η ![]() λέγεται επίθεμα (suffix)
της
λέγεται επίθεμα (suffix)
της ![]() αν υπάρχει
αν υπάρχει ![]() τ.ώ.
τ.ώ.
![]() .
Είναι φανερό ότι μια λέξη με μήκος
.
Είναι φανερό ότι μια λέξη με μήκος ![]() έχει ακριβώς
έχει ακριβώς ![]() προθέματα και άλλα
τόσα επιθέματα.
προθέματα και άλλα
τόσα επιθέματα.


![]() και
και ![]() λέγονται
διαδοζικές αν υπάρχει η ακμή
λέγονται
διαδοζικές αν υπάρχει η ακμή ![]() .
Έτσι, στο σχήμα που φαίνεται παραπάνω το 24231 είναι ένα μονοπάτι
μήκους 4 (το μήκος είναι το πόσες ακμές διανύονται στο μονοπάτι).
Αν αρχή και τέλος του μονοπατιού συμπίπτουν αυτό λέγεται κύκλος,
π.χ. το 424.
.
Έτσι, στο σχήμα που φαίνεται παραπάνω το 24231 είναι ένα μονοπάτι
μήκους 4 (το μήκος είναι το πόσες ακμές διανύονται στο μονοπάτι).
Αν αρχή και τέλος του μονοπατιού συμπίπτουν αυτό λέγεται κύκλος,
π.χ. το 424.
