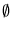 , και
, και
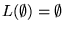
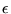 , και
, και
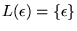
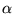 , για κάθε
, για κάθε
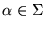 , και
, και
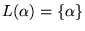 .
.
 , και
, και
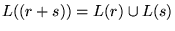
 , και
, και
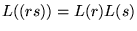 (συγκόλληση των δύο γλωσσών)
(συγκόλληση των δύο γλωσσών)
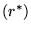 , και
, και
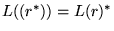 .
.
Θα δώσουμε κατ' αρχήν ένα αναδρομικό ορισμό για το τι είναι μια κανονική έκφραση (regular expression) και το ποια γλώσσα παριστάνει.
Τα παρακάτω είναι παραδείγματα κανονικών εκφράσεων και των γλωσσών τους.
| Κανονική έκφραση | Αντίστοιχη γλώσσα |
|
|
|
| Όλες οι λέξεις πάνω από το
|
|
|
|
Όλες οι λέξεις πάνω από το
|
| Ότι αρχίζει με 1 και δεν έχει διαδοχικά 0 | |
|
|
Ότι δεν έχει διαδοχικά 0 |
| Λέξεις όπου τα 0 έρχονται πριν τα 1 κι αυτά πριν τα 2. |
Παρατηρείστε ότι δεν ξεκαθαρίζουμε τι είδους αυτόματο μια και είναι όλα ισοδύναμα.
Απόδειξη.
Θα δείξουμε ότι (α) Κάθε κανονική γλώσσα αναγνωρίζεται από κάποιο
![]() -NFA, και (β) Η γλώσσα που αναγνωρίζει κάθε DFA είναι κανονική.
-NFA, και (β) Η γλώσσα που αναγνωρίζει κάθε DFA είναι κανονική.
(α) Χρησιμοποιούμε επαγωγή ως προς το μήκος της κανονικής έκφρασης ![]() που παράγει
τη γλώσσα. Αν πρόκειται για μια από τις εκφράσεις
που παράγει
τη γλώσσα. Αν πρόκειται για μια από τις εκφράσεις ![]() ,
, ![]() ή
ή ![]() ,
με
,
με
![]() , πολύ έύκολα φτιάχνουμε αυτόματα που τις αναγνωρίζουν
όως φαίνεται στο παρακάτω Σχήμα 14.
, πολύ έύκολα φτιάχνουμε αυτόματα που τις αναγνωρίζουν
όως φαίνεται στο παρακάτω Σχήμα 14.
Αν τώρα έχουμε μια έφραση ![]() του τύπου
του τύπου ![]() ,
, ![]() η
η ![]() , τότε τα μήκη των
, τότε τα μήκη των ![]() και
και ![]() είναι αυτστηρά μικρότερα του
είναι αυτστηρά μικρότερα του
![]() , άρα μπορούμε να υποθέσουμε επαγωγικά
ότι έχουμε κάποια αυτόματα
, άρα μπορούμε να υποθέσουμε επαγωγικά
ότι έχουμε κάποια αυτόματα ![]() και
και ![]() που αναγνωρίζουν τις γλώσσες
που αναγνωρίζουν τις γλώσσες ![]() και
και ![]() .
Χρησιμοποιούμε τα
.
Χρησιμοποιούμε τα ![]() και
και ![]() σα μαύρα κουτιά και μας ενδιαφέρει μόνο να ``βλέπουμε''
απ' έξω τις αρχικές και τελικές τους καταστάσεις.
σα μαύρα κουτιά και μας ενδιαφέρει μόνο να ``βλέπουμε''
απ' έξω τις αρχικές και τελικές τους καταστάσεις.
Στο Σχήμα 15 βλέπουμε στα (a) και (b) τα
αυτόματα ![]() και
και ![]() που αντιστοιχούν στις εκφράσεις
που αντιστοιχούν στις εκφράσεις ![]() και
και ![]() .
Στα (c), (d) και (e) βλέπουμε πως αυτά συνδυάζονται ώστε να φτιάξουν αυτόματα
για τις γλώσσες
.
Στα (c), (d) και (e) βλέπουμε πως αυτά συνδυάζονται ώστε να φτιάξουν αυτόματα
για τις γλώσσες ![]() ,
, ![]() και
και ![]() .
.
Στο (c) ορίζουμε μια νέα αρχική κορυφή και την ενώνουμε με ![]() -ακμές
με τις δύο αρχικές κορυφές των
-ακμές
με τις δύο αρχικές κορυφές των ![]() και
και ![]() . Οι τελικές καταστάσεις
παραμένουν οι ίδιες.
. Οι τελικές καταστάσεις
παραμένουν οι ίδιες.
Στο (d) αρχική κορυφή είναι αυτή του ![]() του οποίου οι τελικές καταστάσεις
συνδέονται με
του οποίου οι τελικές καταστάσεις
συνδέονται με ![]() -ακμές με την αρχική του
-ακμές με την αρχική του ![]() . Τελικές καταστάσεις του
συμπλέγματος είναι αυτές του
. Τελικές καταστάσεις του
συμπλέγματος είναι αυτές του ![]() .
.
Στο (e) οι τελικές καταστάσεις του ![]() συνδέονται με
συνδέονται με ![]() -ακμές με
την αρχική κατάσταση του
-ακμές με
την αρχική κατάσταση του ![]() . Αρχικές και τελικές καταστάσεις παραμένουν οι ίδιες.
. Αρχικές και τελικές καταστάσεις παραμένουν οι ίδιες.
(β) Έστω DFA
![]() , όπου
, όπου
![]() .
Ορίζουμε για
.
Ορίζουμε για
![]() ,
,
![]() , τις γλώσσες
, τις γλώσσες
![]() να είναι εκείνες οι λέξεις του
να είναι εκείνες οι λέξεις του ![]() που είναι τέτοιες ώστε
αν ξεκινήσουμε από την κορυφή
που είναι τέτοιες ώστε
αν ξεκινήσουμε από την κορυφή ![]() και τις ακολουθήσουμε τότε φτάνουμε στην κορυφή
και τις ακολουθήσουμε τότε φτάνουμε στην κορυφή ![]() χωρίς να χρησιμοποιήσουμε κορυφή
χωρίς να χρησιμοποιήσουμε κορυφή ![]() με
με ![]() .
.
Είναι φανερό ότι
Θα δείξουμε με επαγωγή ως προς το ![]() ότι οι γλώσσες
ότι οι γλώσσες ![]() είναι
όλες κανονικές. Άρα κανονική είναι και η
είναι
όλες κανονικές. Άρα κανονική είναι και η ![]() αφού με βάση
την (4) είναι πεπερασμένη ένωση από κανονικές γλώσσες, και
η ένωση δύο κανονικών γλωσσών είναι εξ ορισμού κανονική.
αφού με βάση
την (4) είναι πεπερασμένη ένωση από κανονικές γλώσσες, και
η ένωση δύο κανονικών γλωσσών είναι εξ ορισμού κανονική.
Για ![]() τώρα, παρατηρούμε ότι η απαίτηση, στον ορισμό της
τώρα, παρατηρούμε ότι η απαίτηση, στον ορισμό της ![]() όσον
αφορά το ποιες κορυφές δεν πρέπει να χρησιμοποιηθούν είναι ιδιαίτερα αυστηρή,
αφού η συνθήκη
όσον
αφορά το ποιες κορυφές δεν πρέπει να χρησιμοποιηθούν είναι ιδιαίτερα αυστηρή,
αφού η συνθήκη ![]() ισχύει για κάθε κορυφή
ισχύει για κάθε κορυφή ![]() . Άρα έχουμε
. Άρα έχουμε
Όσον αφορά το επαγωγικό βήμα, αν υποθέσουμε ότι οι
![]() είνάι όλες
κανονικές τότε το ίδιο συνάγουμε και για τις
είνάι όλες
κανονικές τότε το ίδιο συνάγουμε και για τις ![]() αφού παρατηρήσουμε ότι
ισχύει η αναδρομική σχέση
αφού παρατηρήσουμε ότι
ισχύει η αναδρομική σχέση
Είναι φανερό ότι η γλώσσα ![]() είναι υπερσύνολο της
είναι υπερσύνολο της
![]() ,
αφού ο περιορισμός
,
αφού ο περιορισμός ![]() , στον ορισμό της
, στον ορισμό της ![]() , γίνεται ασθενέστερος (ισχύει
πιο συχνά) όσο μεγαλώνει το
, γίνεται ασθενέστερος (ισχύει
πιο συχνά) όσο μεγαλώνει το ![]() .
Ποιες είναι όμως εκείνες οι λέξεις που ανήκουν στο σύνολο
.
Ποιες είναι όμως εκείνες οι λέξεις που ανήκουν στο σύνολο ![]() αλλά
όχι στο
αλλά
όχι στο
![]() , οι λέξεις με άλλα λόγια της (συνολοθεωρητικής) διαφοράς
, οι λέξεις με άλλα λόγια της (συνολοθεωρητικής) διαφοράς
![]() ;
Είναι ακριβώς εκείνες οι λέξεις που οδηγούν από την κατάσταση
;
Είναι ακριβώς εκείνες οι λέξεις που οδηγούν από την κατάσταση ![]() στην
στην ![]() ,
χωρίς να ``πατούν'' σε κορυφή
,
χωρίς να ``πατούν'' σε κορυφή ![]() ,
, ![]() , αλλά που πατούν τουλάχιστον μια φορά στην
κορυφή
, αλλά που πατούν τουλάχιστον μια φορά στην
κορυφή ![]() όως φαίνεται στο Σχήμα 16.
όως φαίνεται στο Σχήμα 16.
Μια τέτοια λέξη αντιστοιχεί σε ένα μονοπάτι πάνω στο DFA που σίγουρα ``πατάει'' πάνω
στην κορυφή ![]() , ενδεχομένως και πάνω από μία φορά (στο Σχήμα 16 πατάει
δύο φορές). Αν ονομάσουμε
, ενδεχομένως και πάνω από μία φορά (στο Σχήμα 16 πατάει
δύο φορές). Αν ονομάσουμε ![]() μια τέτοια λέξη, και ονομάσουμε
μια τέτοια λέξη, και ονομάσουμε ![]() το πρόθεμα της
το πρόθεμα της
![]() που αντιστοιχεί στο μονοπάτι από το
που αντιστοιχεί στο μονοπάτι από το ![]() στο
στο ![]() , που δεν πατάει στην
, που δεν πατάει στην ![]() ,
και
,
και ![]() το επίθεμα της
το επίθεμα της ![]() γαι το μονοπάτι
γαι το μονοπάτι
![]() που δεν πατάει στην
που δεν πατάει στην ![]() ,
τότε η
,
τότε η ![]() γράφεται
γράφεται