


Next: 5.35 Συν. κατανομής και
Up: 5 Ημερολόγιο διαλέξεων
Previous: 5.33 Όγδοη ομάδα ασκήσεων
Contents
Ορίσαμε τη συνάρτηση κατανομής δύο ΤΜ 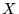 και
και 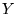 ορισμένων
πάνω στον ίδιο δειγματικό χώρο ως
ορισμένων
πάνω στον ίδιο δειγματικό χώρο ως
Είδαμε απλές ιδιότητες αυτής ανάλογες με τη μονοδιάστατη συνάρτηση κατανομής
(μονοτονία ως προς κάθε μεταβλητή χωριστά, όρια στο 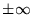 ) και κάποια παραδείγματα.
Είδαμε επίσης τι σημαίνει ότι ένα ζεύγος έχει συνάρτηση πυκνότητας πιθανότητας
) και κάποια παραδείγματα.
Είδαμε επίσης τι σημαίνει ότι ένα ζεύγος έχει συνάρτηση πυκνότητας πιθανότητας
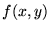 . Είδαμε ότι όταν αυτό συμβαίνει η
. Είδαμε ότι όταν αυτό συμβαίνει η 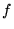 δεν είναι μονοσήμαντα ορισμένη,
καθώς μπορούμε να αλλάξουμε τις τιμές της πάνω σε μια καμπύλη, π.χ., χωρίς να
αλλάξουν τα ολοκληρώματά της, που είναι και οι ποσότητες που ενδιαφέρουν.
δεν είναι μονοσήμαντα ορισμένη,
καθώς μπορούμε να αλλάξουμε τις τιμές της πάνω σε μια καμπύλη, π.χ., χωρίς να
αλλάξουν τα ολοκληρώματά της, που είναι και οι ποσότητες που ενδιαφέρουν.
Κάναμε μια μικρή επανάληψη στα διπλά ολοκληρώματα.
Mihalis Kolountzakis
![]() και
και ![]() ορισμένων
πάνω στον ίδιο δειγματικό χώρο ως
ορισμένων
πάνω στον ίδιο δειγματικό χώρο ως