


Next: 5.33 Όγδοη ομάδα ασκήσεων
Up: 5 Ημερολόγιο διαλέξεων
Previous: 5.31 Ιδιότητες συνέχειας συνάρτησης
Contents
Σήμερα είδαμε με λεπτομέρεια δύο οικογένειες πυκνοτήτων, τις κανονικές και τις
Γάμμα. Είδαμε επίσης πώς ορίζεται η Γάμμα συνάρτηση και αποδείξαμε μερικές
ιδιότητες γι' αυτήν, όπως τη συνασρτησιακή εξίσωση
Είδαμε επίσης πως αν μια ΤΜ 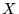 έχει συνάρτηση κατανομής
έχει συνάρτηση κατανομής 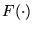 τότε
η ΤΜ
τότε
η ΤΜ 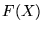 είναι ομοιόμορφη στο
είναι ομοιόμορφη στο 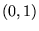 .
Υπό κάποιες γενικές συνθήκες για τη συνάρτηση
.
Υπό κάποιες γενικές συνθήκες για τη συνάρτηση 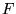 μπορούμε να δείξουμε ότι αν η
μπορούμε να δείξουμε ότι αν η 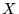 είναι ομοιόμορφη
στο
είναι ομοιόμορφη
στο 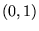 τότε η
τότε η 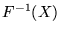 έχει συνάρτηση κατανομής
έχει συνάρτηση κατανομής 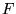 , και αυτός
είναι ένας τρόπος να φτιάχνει κανείς από την ομοιόμορφη κατανομή μια άλλη δεδομένη
κατανομή.
, και αυτός
είναι ένας τρόπος να φτιάχνει κανείς από την ομοιόμορφη κατανομή μια άλλη δεδομένη
κατανομή.
Έγιναν επίσης οι ασκήσεις 39 και 42 του Κεφ. 5.
Mihalis Kolountzakis