


Next: 5.4 Μεταθέσεις και συνδυασμοί,
Up: 5 Ημερολόγιο διαλέξεων
Previous: 5.2 Εισαγωγή στις βασικές
Contents
Είδαμε την έννοια της πιθανότητας υπό συνθήκη. Αν 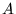 και
και 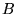 είναι δύο
ενδεχόμενα και
είναι δύο
ενδεχόμενα και
![${{\bf {Pr}}\left[{B}\right]}>0$](img15.png) γράφουμε
γράφουμε
Μια οικογένεια ενδεχομένων 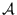 λέγεται ανεξάρτητη αν για κάθε
διαφορετικά ενδεχόμενα
λέγεται ανεξάρτητη αν για κάθε
διαφορετικά ενδεχόμενα
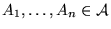 έχουμε
έχουμε
Η έννοια της ανεξαρτησίας μιας οικογένειας ενδεχομένων κωδικοποιεί την
περίπτωση όπου γνώση του αν συμβαίνουν ή όχι κάποια από αυτά δεν επηρεάζει
καθόλου την πιθανότητα να ισχύει ένα άλλο ενδεχόμενο της οικογένειας αυτής.
Είδαμε επίσης ότι αν
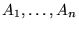 είναι μια διαμέριση του δειγματικού χώρου
είναι μια διαμέριση του δειγματικού χώρου
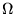 σε σύνολα
σε σύνολα 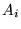 που έχουν θετική πιθανότητα τότε ισχύει (κι είναι πολύ
εύκολο να αποδειχθεί) για κάθε ενδεχόμενο
που έχουν θετική πιθανότητα τότε ισχύει (κι είναι πολύ
εύκολο να αποδειχθεί) για κάθε ενδεχόμενο 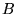
Mihalis Kolountzakis
![]() και
και ![]() είναι δύο
ενδεχόμενα και
είναι δύο
ενδεχόμενα και
![]() γράφουμε
γράφουμε
![]() είναι μια διαμέριση του δειγματικού χώρου
είναι μια διαμέριση του δειγματικού χώρου
![]() σε σύνολα
σε σύνολα ![]() που έχουν θετική πιθανότητα τότε ισχύει (κι είναι πολύ
εύκολο να αποδειχθεί) για κάθε ενδεχόμενο
που έχουν θετική πιθανότητα τότε ισχύει (κι είναι πολύ
εύκολο να αποδειχθεί) για κάθε ενδεχόμενο ![]()
![\begin{displaymath}
{{\bf {Pr}}\left[{B}\right]} = \sum_{i=1}^n {{\bf {Pr}}\left[{B { \vert }A_i}\right]} {{\bf {Pr}}\left[{A_i}\right]}.
\end{displaymath}](img23.png)